1. Akú veľkú prácu musíme vykonať, aby
sme z mydlového roztoku vyfúkli bublinu s priemerom
10cm ? (s = 40.10-3 N.m-1)2. Kapilárou
s vnútorným priemerom 4mm sme odmerali 100 kvapiek
liehu s hmotnosťou 1,81g.
Rovnaké množstvo kvapiek vody s rovnakou teplotou mal
hmotnosť 6,26g. Určte povrchové napätie liehu, ak
povrchové napätie vody je 73.10-3N.m-1.
3. Do akej výšky vystúpi voda (s = 0,0725 N/m) v kapilárnej
rúrke s vnútorným polomerom 1mm ?
[ h = 15 mm]
4. Voda odkvapkáva z kapiláry
s vnútorným priemerom 1,8 mm. Koľko kvapiek vody je v 1cm3
vody?
[ n = 24 kvapiek]
5. V kapilárnej rúrke
s vnútorným priemerom 2 mm je voda. Aký vysoký stĺpec vody zostane v kapiláre
v zvislej polohe, ak obidva jej konce sú otvorené ?
[ h = 3 cm]
6. Kapilárne zvýšenie liehu (r = 0,8 g/cm3,
s = 0,0214 N/m) v úzkej rúrke je
12 mm. Aký veľký je
priemer rúrky ?
[ h = 0,9 mm]
7. Kapilárne zvýšenie vody zo
spodných vrstiev pôdy dosahuje 100 cm. Vypočítajte polomer kapilár
v pôde, za predpokladu, že nie sú prerušené.
Povrchové napätie vody je 0,0725N/m.
[ približne 15 mikrónov]
8. Pri laboratórnej práci žiaci zistili, že v kapilárnej
rúrke s vnútorným priemerom 0,4 mm voda vystúpila do
výšky 7,2 cm nad hladinou vody v nádobe a
v kapiláre s priemerom 0,5 mm petrolej vystúpil do
výšky 2,5 cm. Vypočítajte povrchové napätie vody aj
petroleja zo zistených údajov. (Hustota petroleja je
0,80 kg/l).
[ 0,0706 N/m ; 0,0245 N/m]
9. Koľko
váži kvapka vody, ktorá odkvapla z rúrky priemeru 1
mm ?
[ 23 mg]
10. Určte
povrchové napätie oleja hustoty 0,91 g/cm3,
ak sa pri odkvapkávaní z pipety s vnútorným
priemerom 1,2 mm vytvorilo zo 4 cm3 oleja 304
kvapiek.
[ 0,0312 N/m]
11. Z kapilárnej rúrky odkvapkalo
100 kvapiek vody celkovej hmotnosti 2,4g. Hmotnosť 50 kvapiek glycerínu z tej
istej pipety je 1,1g. Aký je pomer povrchových napätí
obidvoch kvapalín ?
[ 12:11]
12. Akú výšku v musí mať stĺpec liehu v otvorenej
kapilárnej rúrke priemeru 1 mm, aby sa na spodnom konci
kapiláry utvorila kvapka ? Hustota liehu je 0,8 kg/l a
povrchové napätie s = 0,02 N/m.
[ v >
2 cm]
13. Aká veľká povrchová energia sa
uvolní, ak po daždi z kvapiek s priemerom 10-3mm
sa vytvorí veľká kvapka
s priemerom 3 mm ?
[ D A = 6,2 . 10-3J]
14. Akú veľkú prácu musíme vykonať, aby
sme z mydlového roztoku vyfúkli bublinu s priemerom
10 cm ? s = 40.10-3N.m-1
[ A = 2,5 . 10-3J]
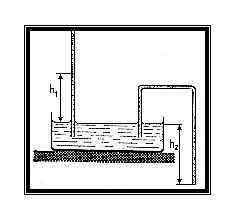 15. Do nádoby
s vodou sú podľa obrázka ponorené dve kapiláry rovnakého vnútorného
priemeru. V rovnej kapiláre vystúpi voda do výšky h1.
Určte tvar menisku a úroveň hladiny vodného stĺpca v ohnutej
kapiláre, ak je ohnutý koniec vo vzdialenosti h2
od vodnej hladiny v nádobe. Uvažujte :
15. Do nádoby
s vodou sú podľa obrázka ponorené dve kapiláry rovnakého vnútorného
priemeru. V rovnej kapiláre vystúpi voda do výšky h1.
Určte tvar menisku a úroveň hladiny vodného stĺpca v ohnutej
kapiláre, ak je ohnutý koniec vo vzdialenosti h2
od vodnej hladiny v nádobe. Uvažujte :
a) h2 > h1
b) h2 = h1
c) h2 < h1
d) h2 = 0
e) h2< 0 , t.j. koniec ohnutej kapiláry je
nad úrovňou vodnej hladiny v nádobe.
[ a)
kapilárne sily môžu
udržať v kapiláre iba stĺpec výšky h. Preto bude
voda z kapiláry vytekať. b) voda nevyteká, meniskus
je vypuklý, c) voda nevyteká, meniskus je menej
vypuklý ako v b), d)voda nevyteká, meniskus je
plochý, e) voda nevyteká, meniskus je dutý]
16. Kapilára má
vnútorný priemer 0,2 mm. Vypočítajte :
a) Ako vysoko v nej stúpne
benzén, keď jeho teplota je 18OC a
hustota r = 870 kg.m-3
?
b) Ako sa zmení výsledok pokusu, ak použijeme kapiláru
s dvojnásobným priemerom ?
c) Ako by sa zmaenil
výsledok pokusu s pôvodnou kapilárou, keby pokus
vykonali na Mesiaci, kde je gravitačné zrýchlenie asi
6-krát menšie ako tiažové zrýchlenie ?
d) Ako by prebiehal pokus
v družici v beztiažovom stave ?
e) Zmení sa dĺžka stĺpca
v kapiláre, ak kapiláru nakloníme pod uhlom 30O
vzhľadom ku kapiláre ?
[ a) h1 = 6,8 cm,
b) h2 = 3,4 cm, c) h3 = 40,8 cm, d)
h4 = ® Y , e) l5 = 13,6 cm ]
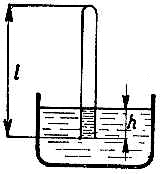
Riešené úlohy náročnejšieho charakteru1.
Sklenená kapilára s vnútorným priemerom d
a dĺžke l
je na jednom konci zatavená. Druhým koncom je ponorená do vody tak,
že jej pozdĺžna os je zvislá a povrchy vody vonku a vo
vnútri kapiláry sú v rovnakej výške. Časť kapiláry pod
vodou označíme h.
Aké veľké je povrchové napätie vody voči vzduchu ?
Riešte najprv všeobecne, potom pre hodnoty: d = 2.10-4m,
l = 2.10-1m, h = 2,9.10-3m,
barometrický tlak je b = 105 N.m-2
Označenie veličín :
Vo – objem kapiláry
p – tlak vo vnútri kapiláry po jej ponorení do vody
V – objem neponorenej časti
s – povrchové napätie vody voči vzduchu
Riešenie :
Súčin objemu
a tlaku vzduchu v kapiláre pred jej ponorením do vody
je 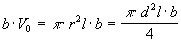 (1)
(1)
Po ponorení kapiláry do vody je sila povrchového
napätia v rovnováhe s tlakovou silou, spôsobenou
pretlakom vzduchu, ktorý je uzavretý v trubici, vzhľadom k atmosferickému tlaku.
Preto platí rovnica 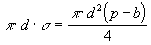 , z ktorej vypočítame p. Po
úprave tejto rovnice dostaneme
, z ktorej vypočítame p. Po
úprave tejto rovnice dostaneme 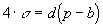 a odtiaľ
a odtiaľ 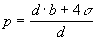 (2)
(2)
Súčin objemu a tlaku
vzduchu vo vnútri kapilárnej trubice má potom hodnotu
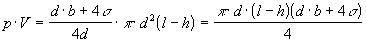
Pretože teplota vzduchu
v kapiláre zostáva rovnaká ako pred ponorením
kapiláry do vody, dostaneme po porovnaní poslednej
rovnice a rovnice (1) vzťah 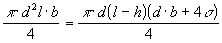 ,
z ktorého po úpravách dostaneme
,
z ktorého po úpravách dostaneme
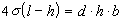
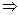
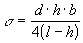 .
.
Výsledok :
Kapilárna konštanta vody je všeobecne určená vzťahom (3) a má hodnotu
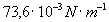 .
.
2. Dve sklenené
kapilárne trubice s priemerom d1,
d2 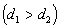 sú čiastočne ponorené zvisle do
kvapaliny s hustotou ? a s povrchovým
napätím ?.
sú čiastočne ponorené zvisle do
kvapaliny s hustotou ? a s povrchovým
napätím ?.Určte vzdialenosť povrchov
obidvoch kvapalín v trubiciach :
pre teplotu vody t,
ortuť s rovnakou
teplotou t.
Riešte najprv všeobecne, potom pre hodnoty d1=
2 mm, d2= 0,6 mm a t
= 18 oC. Hodnoty
povrchových napätí a hustoty vody a ortute pri danej
teplote vyhľadajte
v tabuľkách.
Označenie
veličín a ich hodnoty :
Povrchové napätie označíme s,
hustotu kvapaliny r.
Pri teplote 18oC
má voda povrchové napätie 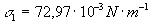 , ortuť rovnakej teploty
, ortuť rovnakej teploty 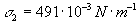 .
Hustota vody pri teplote 18oC je
.
Hustota vody pri teplote 18oC je 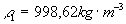 ,
ortute
,
ortute 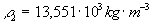 .
.
Pôsobením stykového napätia na rozhraní kvapaliny
a steny kapilárnej trubice nastáva u kvapalín,
ktoré zmáčajú steny
trubice kapilárna elevácia (obr.1), u kvapalín,
ktoré nazmáčajú steny trubice, kapilárna depresia
(obr.2)
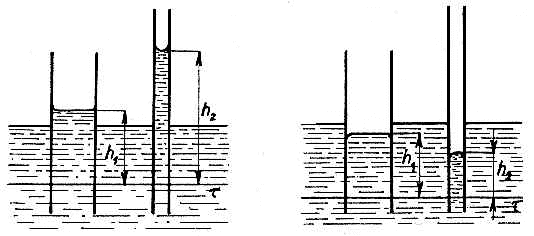
Veďme
v ľubovoľnej hĺbke pod povrchom kvapaliny v obidvoch
kapilárnych trubiciach vodorovnú rovinu ?, a ak
označíme výšky povrchov kvapaliny nad rovinou ? v širšej
kapilárnej trubici h1, v užšej h2,
je rozdiel vzdialenosti povrchov kvapaliny v týchto
trubiciach 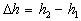 u kvapalín, ktoré zmáčajú steny trubice a
u kvapalín, ktoré zmáčajú steny trubice a 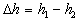 u kvapalín, ktoré nezmáčajú
steny trubice.
u kvapalín, ktoré nezmáčajú
steny trubice.
Tlaky
kvapaliny v širšej trubici v hĺbke h1
označíme p1,
v užšej trubici v hĺbke h2, písmenom p2.
Barometrický tlak označíme b, tiažové
zrýchlenie 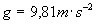 .
.
Riešenie :
Ak označíme písmenom
S prierez trubice valcovitého tvaru s priemerom d,
má tlaková sila v kvapaline s hustotou ? m? tlakov?ča steny trubice
v hĺbke h pod povrchom kvapaliny
v trubici hodnotu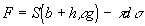 , ako vidieť z obr.1 Pôsobí teda v rovine ?
ktorá
sa nachádza v hĺbke h
pod povrchom kvapaliny, ktorá zmáča steny trubice tlak
, ako vidieť z obr.1 Pôsobí teda v rovine ?
ktorá
sa nachádza v hĺbke h
pod povrchom kvapaliny, ktorá zmáča steny trubice tlak 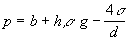 (1)
(1)
Pre kvapaliny, ktoré zmáčajú
steny platí za rovnakých okolností podľa obr.2 vzťah 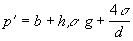 (2)
(2)
U kvapalín, ktoré zmáčajú steny trubice :
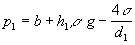 a obdobne
a obdobne 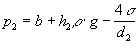
Pretože v trubiciach je
rovnováha, je 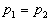 , takže platí
, takže platí 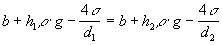 ,
odtiaľ
,
odtiaľ
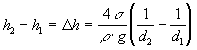 (3)
(3)
U kvapalín, ktoré nezmáčajú steny trubice
:
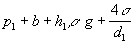 a obdobne
a obdobne 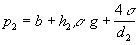 , odtiaľ
, odtiaľ
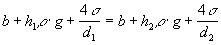 , odtiaľ
, odtiaľ
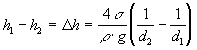 ako v prípade (1).
ako v prípade (1).
Ak dosadíme do (1) dané hodnoty, pre vodu
dostaneme
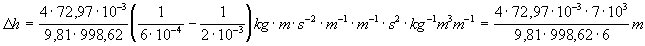
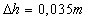
Pre ortuť
dostaneme
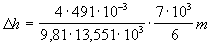
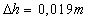
Výsledok :
Rozdiel povrchov kvapalín v obidvoch kapilárnych
trubiciach je za daných podmienok u vody 3,5cm
a u ortuti 1,9cm. Všeobecne je hodnota tohoto rozdielu
určená vzťahom (3).