Pascalov zákon

1.    Vypočítajte priemer veľkého piesta hydraulického zdviháka v autoservise Qualt Košice, ak je priemer malého piesta olejového čerpadla d = 14 mm a tlak v hydraulickom  systéme je 16 MPa. Maximálna povolená hmotnosť nákladu sú  2 t.

2.    V hydraulickom zariadení zubárskeho kresla je piest s obsahom plochy 65 cm². Kreslo má hmotnosť 50kg. Akou silou bude musieť pôsobiť  zubár na tlačidlo malého piesta s obsahom 3,25 cm², v prípade, že vás bude chcieť  zodvihnúť  ? Akú prácu vykoná, ak vás zodvihne o 0,15 m ? 

3.    Piest automobilového zdviháku má priemer d = 150 mm. Aký veľký musí byť tlak oleja v hydraulickom systéme, ak pomocou zdviháku chceme  zodvihnúť Škodu Felíciu ?

4.    Pri dvíhaní nákladu s hmotnosťou 2000 kg pomocou hydraulického zariadenia sa vykonala práca 40 J. Malý piest vykonal pri dvíhaní nákladu 10 zdvihov, pri jednom zdvihu sa posunul o 10 cm. V akom pomere sú obsahy plôch veľkého a malého piesta ? 

 5.    Zadná náprava nákladného auta, na ktorú pôsobí tlaková sila 2,25.10⁴ N má byť zodvihnutá hydraulickým zdvihákom. Stačí pôsobiť silou 160 N na menší piest, ak prevodový pomer zdviháku je 140 : 1 ? 

6.    Ako sa zmení tlaková sila veľkého piestu v hydraulickom lise, ak polomer malého piestu zmenšíme na r/2, r/3, r/4, r/5....?   Situáciu znázornite graficky. 

7.    Vypočítajte dĺžku zdvihu malého piesta, ak je zdvih veľkého piestu 25 cm a pomer síl v hydraulickom zariadení 1 : 180. 

Hydrostatický tlak

8.    Do jedného ramena U - trubice, v ktorej je ortuť, nalejeme vodu a vpustíme železnú guličku s hmotnosťou m. O akú výšku  vystúpi ortuť v druhom ramene trubice ? Obsah prierezu U - trubice je S, objem naliatej vody je V. Riešte najprv všeobecne a potom pre konkrétne, vami zadané hodnoty.     

9.    Toricelli použil pri svojom pokuse ortuť. Akú vysokú sklenenú trubicu by musel použiť, ak by na svoj pokus použil vodu ? Uvažujte, že pokus by realizoval za normálneho atmosférického tlaku.  

10.    Hladina vody vo vodojeme je vo výške 34 m. Aký je tlak studenej vody v potrubí pri kohútiku vo vašej  kuchyni ? 

11.    Aký rozdiel hladín ukazuje otvorený manometer pri pretlaku 0,1 atm ak je plnený ortuťou ( vodou ) ?

 12.    Aký minimálny tlak musí vyvinúť pumpa, aby dopravila vodu do výšky 24 m pod tlakom 10⁵ Pa ?

 13.    Pohár  naplnený až po okraj  vodou prikryjeme kúskom  papiera a obrátime hore dnom. Papier neodpadne. Vypočítajte veľkosť  sily, ktorá pridržiava papier o pohár. Zvoľte si vlastné rozmery podľa konkrétneho prípadu.  

 14.    Pri výrobe ocele sa tryskami pri dne konvertora fúka do tekutého železa stlačený vzduch. Aký najmenší tlak musí mať vzduch, ak tekuté železo v konvertore má výšku 1,4 m ? Uvažujte hustotu železa 7600 kg.m^-3.

Archimedov zákon

15.    Skúmavku naplňte istým počtom rovnakých sklenených guličiek tak, aby plávala vo vode vo zvislom smere. Odmerajte l₁ - vzdialenosť horného okraja skúmavky od hladiny vody v nádobe. Pridajte 10 rovnakých sklenených guličiek a odmerajte l₂ - vzdialenosť horného okraja skúmavky od hladiny vody v nádobe. Vonkajší priemer skúmavky je d. Popíšte ako z nameraných údajov vypočítate hmotnosť  jednej  sklenenej  guličky.   

16.    Ľadová kryha tvaru dosky všade rovnakej hrúbky pláva na hladine jazera. Má hrúbku 20 cm, plošný obsah 4 m², Hustota ľadu je 920 kg.m^-3, hustota vody je 1000 kg. m^-3.
a.    V akej vzdialenosti od hladiny vody je horná plocha kryhy ?
b.    Aká bude vzdialenosť hornej plochy kryhy od hladiny vody, ak na ňu položíme teleso s hmotnosťou 20 kg ?
c.    Akú maximálnu záťaž kryha unesie ? 

17.    V nádobke od jogurtu Sajo je oceľová gulička. Nádobka pláva v odmernom valci s vodou. Fixou označíme výšku vodnej hladiny vo valci. Guličku vysypeme do vody a nádobku opäť necháme plávať na vode.
a.    Ako sa zmení výška vodnej hladiny ?
b.    Ako  by sa zmenila  výška vodnej hladiny, ak by sme mali v  nádobke naliatu vodu?
c.    Ako by sa zmenila výška vodnej hladiny, ak by sme mali v nádobke kúsok dreva ?  

 18.    Nádoba je vyrobená z plechu s hustotou 7700 kg.m^-3 a má hmotnosť 0,5 kg a vnútorný objem 1 l. Položíme ju na voľný povrch vody. Koľko vody môžeme naliať do nádoby, aby sa úplne neponorila ?

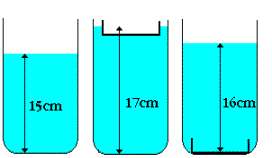
19.    V nádobe s obsahom  dna 150 cm², je naliata voda do výšky 15 cm nad dno nádoby. Ak vložíme do nádoby  misku, vystúpi voda do výšky 17 cm. Po ponorení misky do vody je hladina vody vo výške 16 cm. Určte hmotnosť misky a materiál, z ktorého je vyrobená.    

20.  V nádobe sa nachádza ortuť a nad ňou je naliata voda. V ortuti pláva železná kocka so stranou 5 cm. Sústava je v  rovnováhe.
a)    Vypočítajte, akou časťou je kocka ponorená do ortuti a akou do vody.
b)   Ako sa bude meniť ponor kocky, ak budeme dolievať vodu ?
c)    Nakreslite graf závislosti ponoru kocky v ortuti od množstva prilievanej vody.

 21.    Na konci rovnorodej tyčky s hmotnosťou 4 g je na niti zavesená hliníková gulička s polomerom 0,5 cm. Tyčinka je umiestnená  na okraji tenkostenného pohára s vodou tak, že je v rovnováhe, ak je gulička ponorená polovicou svojho objemu do vody. V akom pomere sú ramená l₁, l₂ ak je splnená podmienka rovnováhy ?

22.    Valcová plechová nádoba s vonkajším polomerom 0,1 m pláva vo vode tak, že vyčnieva 0,1 m nad hladinu vody v prípade, že je o jej dno pripevnené železné závažie s hmotnosťou 1 kg. Ako vysoko bude vyčnievať nádoba z vody v prípade, že závažie premiestnime dnu do nádoby ?

23.    Nákladná loď s celkovou hmotnosťou 4500 t vypláva z rieky na more. O koľko ton je možné zvýšiť hmotnosť nákladu lode v prípade, že zachováme ponor lode nezmenený ?

24.    Odliatok zliatiny hliníka a horčíka je na vzduchu vyvážený závažím  s hmotnosťou 3,6 kg a vo vode závažím s hmotnosťou 1,6 kg. Určte hustotu zliatiny. Aké je percentuálne zloženie zliatiny ?

25.    Balón s polomerom 4 m  naplnený héliom sa vznáša v konštantnej výške vo vzduchu s teplotou -23^oC a tlaku 0,5.10⁵ Pa. Akou silou je nadľahčovaný balón, ak hustota hélia je 0,0098 kg.m^-3 a hustota vzduchu je 0,0707 kg.m^-3 ?

26.    Akou časťou svojho objemu trčí plávajúca ľadová kryha nad hladinu morskej vody ?

27.    Majme veľké množstvo valcových sudov, vložených do seba tak, že každý pláva v predchádzajúcom. Plocha dna najmenšieho z nich je omnoho menšia ako plocha najväčšieho z nich. Do najmenšieho suda nalejeme vodu s objemom V₀ tak, že všetky sudy ostanú plávať. O koľko sa posunie dno tohto suda oproti zemi ?

28.    Plochý drevený kváder s výškou 4 cm sa ponorí v benzíne ( r = 0,7 g.cm^-3) o 8 mm hlbšie ako vo vode. Akú hustotu má drevo ?

29.    Akú hrúbku má mať mosadzný (r = 8,6 g.cm^-3) plech na vyhotovenie plaváka karburátora, keď v benzíne (r = 0,75 g.cm^-3) plávajúci plavák má 1/4 svojej výšky vyčnievať ? Plavák je valcový, 4 cm vysoký a má priemer 5 cm.

30.    Drevená ( r = 705 kg.m^-3) konštrukcia s tiažou 200 kg má byť ponorená vo vode a zaťažením kameňmi ( r = 2507 kg.m^-3) sa má zabrániť jej vynoreniu. Aké najmenšie množstvo kameňov ( čo do hmotnosti ) budeme potrebovať ?

31.    Plocha priečneho rezu lode vo výške ponoru je 3800 m². Po naložení nákladu sa ponor lode zväčšil o 2m. Aký ťažký je náklad lode, keď hustota morskej vody je ( r = 1002 kg.m^-3 ) ?

32.    V nádobe je naliata voda a na vode olej hustoty ( r = 600 kg.m^-3). V týchto kvapalinách je úplne ponorená drevená kocka s hranou 10 cm a pláva tak, že je 2 cm pod rozhraním vody s olejom.

a)  Aká je hmotnosť kocky ?