1.
Akú
veľkú prácu musíme vykonať, aby sme z mydlového roztoku vyfúkli
bublinu s priemerom 10cm? (s
= 40.10-3 N.m-1)
2.
Kapilárou
s vnútorným priemerom 4mm sme odmerali 100 kvapiek liehu s hmotnosťou
1,81g. Rovnaké množstvo kvapiek vody s rovnakou teplotou malo
hmotnosť 6,26g. Určte povrchové napätie liehu, ak povrchové napätie
vody je 73.10-3N.m-1.
3.
Do
akej výšky vystúpi voda (s
= 0,0725 N/m) v kapilárnej rúrke s vnútorným polomerom 1
mm ? [h
= 15 mm]
4.
Voda
odkvapkáva z kapiláry s vnútorným priemerom 1,8 mm. Koľko
kvapiek vody je v 1 cm3 vody?
[n
= 24 kvapiek]
5.
V kapilárnej
rúrke s vnútorným priemerom 2 mm je voda. Aký vysoký stĺpec
vody zostane v kapiláre v zvislej polohe, ak obidva jej konce
sú otvorené ? [h = 3 cm]
6.
Kapilárne
zvýšenie liehu (r
= 0,8 g/cm3, s
= 0,0214 N/m) v úzkej rúrke je 12 mm. Aký veľký je priemer rúrky
? [h = 0,9 mm]
7.
Kapilárne
zvýšenie vody zo spodných vrstiev pôdy dosahuje 100 cm. Vypočítajte
polomer kapilár v pôde, za predpokladu, že nie sú prerušené.
Povrchové napätie vody je 0,0725 N/m.[približne
15 mikrónov]
8.
Pri
laboratórnej práci žiaci zistili, že v kapilárnej rúrke s vnútorným
priemerom 0,4 mm voda vystúpila do výšky 7,2 cm nad hladinou vody v nádobe
a v kapiláre s priemerom 0,5 mm petrolej vystúpil do výšky
2,5 cm. Vypočítajte povrchové napätie vody aj petroleja zo zistených
údajov. (Hustota petroleja je 0,80 kg/l).
[0,0706
N/m ;
0,0245 N/m]
9.
Koľko
váži kvapka vody, ktorá odkvapla z rúrky priemeru 1 mm ? [23
mg]
10.
Určte
povrchové napätie oleja hustoty 0,91 g/cm3, ak sa pri
odkvapkávaní z pipety s vnútorným priemerom 1,2 mm
vytvorilo zo 4 cm3 oleja 304 kvapiek.
[0,0312
N/m]
11.
Z kapilárnej
rúrky odkvapkalo 100 kvapiek vody celkovej hmotnosti 2,4g. Hmotnosť 50
kvapiek glycerínu z tej istej pipety je 1,1g. Aký je pomer
povrchových napätí obidvoch kvapalín ?
[12:11]
12.
Akú
výšku v musí mať stĺpec liehu v otvorenej kapilárnej rúrke
priemeru 1 mm, aby sa na spodnom konci kapiláry utvorila kvapka ?
Hustota liehu je 0,8 kg/l a povrchové napätie s
= 0,02 N/m. [v
>
2 cm]
13.
Aká
veľká povrchová energia sa uvolní, ak po daždi z kvapiek s priemerom
10-3mm sa vytvorí veľká
kvapka s priemerom 3 mm ?
[DA = 6,2 . 10-3J]
14.
Akú
veľkú prácu musíme vykonať, aby sme z mydlového roztoku vyfúkli
bublinu s priemerom 10 cm ?
s
= 40.10-3N.m-1
[A = 2,5 . 10-3J]
15.
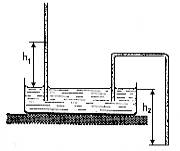
Do
nádoby s vodou sú podľa obrázka ponorené dve kapiláry rovnakého
vnútorného priemeru. V rovnej kapiláre vystúpi voda do výšky h1. Určte tvar menisku a úroveň hladiny vodného stĺpca
v ohnutej kapiláre, ak je ohnutý koniec vo vzdialenosti h2
od vodnej hladiny v nádobe. Uvažujte :
a.
h2
> h1
b.
h2
= h1
c.
h2
<
h1
d.
h2
= 0
e.
h2<
0 , t.j. koniec ohnutej kapiláry je nad úrovňou vodnej hladiny v nádobe.
[a)
kapilárne sily môžu udržať v kapiláre iba stĺpec výšky h.
Preto bude voda z kapiláry vytekať. b)voda nevyteká, meniskus je
vypuklý, c) voda nevyteká, meniskus je menej vypuklý ako v b), d)
voda nevyteká, meniskus je plochý, e) voda nevyteká, meniskus je dutý]
16.
Kapilára
má vnútorný priemer 0,2 mm. Vypočítajte :
a.
Ako vysoko v nej stúpne benzén, keď jeho teplota je 18OC
a hustota r
= 870 kg.m-3 ?
b.
Ako sa zmení výsledok pokusu, ak použijeme kapiláru s dvojnásobným
priemerom ?
c.
Ako by sa zmenil výsledok pokusu s pôvodnou kapilárou, keby
pokus vykonali na Mesiaci, kde je gravitačné zrýchlenie asi 6-krát menšie
ako tiažové zrýchlenie ?
d.
Ako by prebiehal pokus v družici v beztiažovom stave ?
e.
Zmení sa dĺžka stĺpca v kapiláre, ak kapiláru nakloníme pod
uhlom 30O vzhľadom ku kapiláre ?
[a)
h1 = 6,8 cm, h2
= 3,4 cm, h3 = 40,8
cm, h4 = ®µ,
h5 = 13,6 cm ]
17.
Sklenená kapilára s vnútorným priemerom d a s dĺžkou l je na
jednom konci zatavená. Druhým koncom je ponorená do vody tak, že jej
pozdĺžna os je zvislá a povrchy vody vonku a vo vnútri kapiláry
sú v rovnakej výške. Časť kapiláry pod vodou označíme h. Aké
veľké je povrchové napätie vody voči vzduchu ?
O
atómoch a molekulách
18.
Koľko molov ľudi žije na Zemi ?
19.
Vypočítajte počet molekúl vody v 100 ml vody.
20.
Aký objem zaberá 1mol vzduchu, vody, železa ?
21.
Koľko atómov olova je v jednom broku do vzduchovky ?
22.
Kryštál soli NaCl má jednoduchú kubickú mriežku. Určte priemernú
vzdialenosť medzi stredmi iónov.
23.
Akú vzdialenosť by sme dosiahli ak by sme poukladali vedľa seba všetky
atómy obsiahnuté v 1 g vody ? Vzdialenosť vyjadrite v AU.
24.
Akú veľkú plochu by zaberali atómu 1cm3 medi, ak by sme
ich vylisovali tak, že by vytvárali jednoatómovú vrstvu ( atómy považujte
za kocky uložené tesne vedľa seba ) ?
25.
Kryštálová mriežka železa je kubická, priestorovo centrovaná. Určte
na základe tabuľkových hodnôt mriežkovú konštantu železa.
26.
Porovnajte kinetické energie molekúl kyslíka a vodíka, keď ich rýchlosti
pri teplote 20oC sú 1840 m.s-1 a 460m.s-1.
Deformácia
pevných látok
27.
Ako sa zmení napätie drôtu, ak napínaciu silu zväčšíme 4x a
priemer drôtu zväčšíme 2x ?
28.
Oceľová skušobná tyčinka s priemerom 15mm sa pretrhla pôsobením
sily 1,63.105 N. Určte medzu pevnosti ocele v ťahu.
29.
Zistite
nosnosť niektorého z výťahov, ktorý používate. Odhadnite hmotnosť
kabíny a navrhnite počet a hrúbku oceľových lán, na ktorých sa bude
výťah pohybovať tak, aby ste sa v ňom cítili bezpečne.
30.
Vypočítajte
Youngov modul pružnosti v ťahu drevenej dosky pre skok do vody, ktorá má
rozmery : dĺžka 1,8m, šírka 30 cm, výška 5 cm, ak sa pri zaťažení
silou 600 N na voľnom konci ohne o 4 cm.
31.
Vlaková
koľajnica bola zvarená pri teplote 20oC. Vypočítajte, či
sa neprekročí medza pevnosti v ťahu použitej ocele ( 220MPa), ak
teplota okolia bude kolísať v rozpätí -20oC až 40oC.
32.
Uvažujte
reálnu gitaru za predpokladu, že dve susedné struny sú oceľové a majú
rovnakú dĺžku a priečny prierez. Koľkokrát väčšia ( menšia ) napínacia
sila musí pôsobiť na strunu vydávajúcu tón d voči strune vydávajúcej
tón c ? Rozdiskutujte reálnu situáciu.
