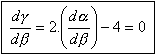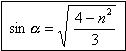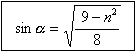FYZIKA |
|
Školský
Informačný
|
|
|||||||||||||||||
|
Dúha
nesporne patrí k najnápadnejším a najkrajším prírodným úkazom. O
jej popis sa oddávna usilovali básnici i vedci. Fyzikálne vysvetlenie dúhy
sa pritom často považuje za jednoduchý problém geometrickej optiky, ktorý
bol už dávno vyriešený a dnes môže byť zaujímavý iba z hľadiska
histórie. V skutočnosti to tak nie je – uspokojivá teória
dúhy bola vybudovaná iba nedávno. Táto teória potrebuje omnoho viac
než obyčajnú geometrickú optiku – využíva aj vlnové vlastnosti
svetla, ako je interferencia, difrakcia a polarizácia, aj jeho korpuskulárne
vlastnosti, napr. hybnosť svetelného zväzku. Z histórie o popisovaní dúhy Prvý
pokus vysvetliť jav dúhy patrí pravdepodobne Aristotelovi
(4. stor. pred n. l.). Vyslovil názor, že dúha je zvláštnym druhom
odrazu slnečného svetla od mrakov. Pretože svetlo sa odráža pod určitým
konštantným uhlom, vzniká kruhový kužeľ „dúhových lúčov“.
Aristoteles tak správne objasnil kruhový tvar oblúka. Tiež postrehol, že
nejde o materiálny objekt v danom mieste oblohy, ale o súhrn smerov, v ktorých
je svetlo rozptyľované do oka pozorovateľa.
Od Aristotelovej domnienky uplynulo takmer sedemnásť storočí, než bol v teórií dúhy vykonaný ďalší podstatný pokrok. V roku 1304 nemecký mních Theodorik z Freibergu zavrhol Aristotelovu hypotézu, že dúha je dôsledkom hromadného odrazu svetla od vodných kvapiek v mraku. Tvrdil, že dúhu dokáže vytvoriť každá vodná kvapka sama o sebe. Dokonca túto ideu experimentálne overil so zväčšenou vodnou kvapkou – použil fľaše tvaru gule naplnené vodou. Theodorikove
zistenia zostali zabudnuté tri storočia, až kým ich nezávisle na ňom
urobil René Descartes
(17. stor. n. l.). Ten použil
rovnakú metódu. Theodorik i Descartes si tiež všimli, že v každom
smere v uhlovom rozmedzí dúhy môžeme vo svetle rozptýlenom guľou
vidieť len jednu farbu. Z toho Theodorik a Descartes usúdili, že každá
farba v dúhe pochádza z iných vodných kvapiek.
Descartes
s Newtonom dokázali vysvetliť všetky nápadnejšie charakteristické
rysy dúhy. Objasnili existenciu primárneho a sekundárneho oblúka i tmavého
pásu, ktorý ich oddeľuje. Vypočítali ich uhlovú polohu a popísali
disperziu rozptyleného svetla do spektrálnych farieb. Ich teória však mala
jeden podstatný nedostatok – nevedela vysvetliť tzv. nadpočetné prúžky,
ktoré sa vyskytujú na vnútornej strane primárnej dúhy. Optický jav objasňujúci vznik
nadpočetných prúžkov objavi v r. 1803 Thomas Young. Ukázal, že
svetlo môže vykazovať interferenciu, čiže jav, ktorý bol už vtedy známy.
Youngova interferenčná teória dúhy dokázala teda vysvetliť všetky
podstatnejšie rysy dúhy. Stále však chýbala matematická teória schopná
predpovedať intenzitu rozptyleného svetla ako fukciu veľkosti kvapiek a
rozptylového
uhla. V roku 1835 poukázal
Richard Potter na to, že pretínaním rôznych sústav lúčov v kvapke
vznikajú tzv. kaustické krivky. Kaustika predstavuje obálku sústavy lúčov
a je vždy spojená so zosilnením intenzity svetla. A tak stanovenie
intenzity rozptyleného svetla v dúhe je podobné riešeniu problému nájdenia
priebehu intenzity v blízkosti kaustiky. V roku 1838 sa pokúsil určiť
tento priebeh Potterov kolega George B. Airy. Jeho úvaha bola založená na
princípe šírenia vĺn sformulovanému v 17. storočí Christianom Huygensom
a prepracovanom neskoršie A. J. Fresnelom. Airy dokázal vyjadriť intenzitu
rozptyleného svetla v dúhe pomocou novej matematickej funkcie – dnes
nazývanej Airyho funkcia. Matematický tvar tejto funkcie je zložitý. Analógiu medzi geometrickou
optikou a klasickou mechanikou častíc postrehol írsky matemetik W. R.
Hamilton už v roku 1831. Lúčom v geometrickej optike sú
analogické trajektórie častíc. Zmene smeru svetelného lúča pri vstupe
do prostredia s iným indexom lomu odpovedá odchýlenie pohybujúcej sa
častice pôsobením síl. Uvažujme vzájomnú zrážku
dvoch atómov plynu, ktoré sa k sebe približujú z počiatočne veľkej
vzdialenosti. Najprv sú k sebe priťahované stále silnejšie. Akonáhle
sa však k sebe priblížia, začnú sa prekrývať ich elektrónové
obaly a príťažlivé sily klesajú. V tesnej blízkosti potom
naopak dôjde k rastúcemu odpudzovaniu. Rovnako ako v prípade
optiky môžeme atómový rozptyl analyzovať sledovaním dráhy atómov v závislosti
od zameriavacieho parametra (Obrázok 6). Vlnovo-mechanické chápanie atómovej
a jadrovej dúhy formulovali v roku 1959 K. W. Ford a
J. A. Wheeler. V dôsledku interferencie medzi atómami vystupujúcimi po
trajektóriách v tom istom smere vznikajú nadpočetné maximá
intenzity. Pre rozptyl častíc bola tiež odvodená analógia Airyho teórie. Atómovú dúhu po prvýkrát
pozorovali E. Hundhausen a H. Pauly v roku 1964 pri rozptyle vodíkového
atómu na atómoch orute. Je iróniou, že tak zložitý
problém ako je dúha, má v skutočnosti presné riešenie. Toto riešenie
je dlhé roky už známe. Akonáhle J. C. Maxwell predložil zhruba pred sto
rokmi elektromagnetickú teóriu svetla, bolo možné problém optickej dúhy
presne matematicky formulovať. Ide o rozptyl elektromagnetického vlnenia
na homogénnej guli. Základné princípy vzniku dúhy
Žiariaci oblúk, ktorý
pozorujeme pri daždi na oblohe alebo vo vodnej triešti vodopádu,
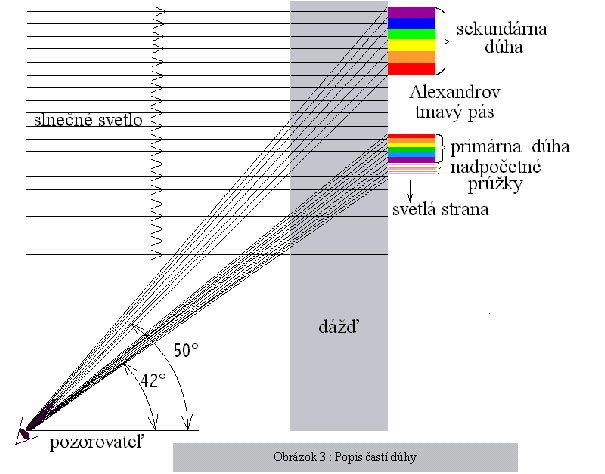
predstavuje primárnu dúhu (Obrázok 1). Jej najnápadnejším rysom
je farebnosť. Jas a zreteľnosť farebných pásov sa môže značne meniť,
ale poradie farieb zostáva stále rovnaké: najvnútornejšia je fialová a tá
prechádza postupne do rôznych odtieňov modrej, zelenej, žltej a oranžovej,
až na vonkajšom okraji je červená (Obrázok 3).
Hlavné
Rysy dúhy je možné pochopiť na základe úvah o
svetle prechádzajúcom jednou vodnou kvapkou. Základné princípy, ktoré
určujú ich podstatu, sú zákony odrazu a lomu svetla. Predbežný rozbor dúhy
spočíva v ich aplikácií na prechod svetelného lúča kvapkou vody.
Tento vnútorný odraz spôsobí
ďalšie odchýlenie o uhol (1800 - 2b) od smeru úsečky AB. Lúč potom
dopadne na povrch kvapky v bode C znova pod uhlom b (vzhľadom k normále).
Tam sa lúč láme a vychádza z kvapky pod tým istým uhlom a, ako do
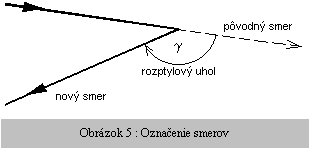
nej vstupoval. A znova spôsobuje odchýlenie o uhol (a - b). Celkový
rozptylový uhol g (Obrázok 5) je potom daný vzťahom:
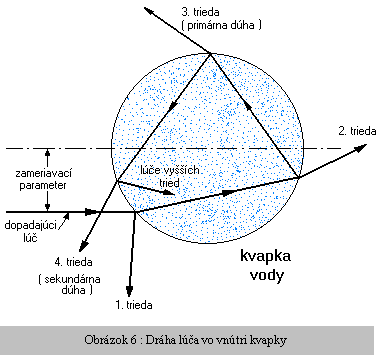
Lúče 1. triedy predstavujú
priamy odraz od kvapky. Lúče 2. triedy cez kvapku priamo prechádzajú. Lúče
3. triedy, ktoré vychádzajú z kvapky po jedinom vnútornom odraze,
tvoria primárnu dúhu. Z lúčov 4. triedy, ktoré podstupujú dva vnútorné
odrazy, vzniká sekundárna dúha. Dúhy vyšších rádov sú tvorené lúčmi
s ešte zložitejším priechodom kvapkou, ale nie sú spravidla viditeľné.
Po jednom vnútornom odraze je rozptylový uhol daný vzťahom
(1). Pre minimálny rozptylový uhol výpočty ukazujú, že dg/da alebo dg/db
musí byť rovná nule. Teda
kde n je index lomu vody. Diferencovaním tohoto vzťahu podľa b dostaneme:
alebo
s ohľadom na substitúciu vo vzťahu
(2). Umocnením a využitím vzťahov (3) a (4) dostávame nový vzťah
vzhľadom
na to , že sin2b+cos2b = 1. Použitím ekvivalentného vzťahu
cos2a=sin2–1 na pravej strane rovnosti (5) získame vzťah:
z ktorého vyplýva: To je sínus uhla dopadu, pri ktorom nastáva minimálny rozptylový uhol a vzniká najkrajšia dúha. Maximálny rozptylový uhol môže byť 180° (kedy a = 0° čiže lúč dopadá v smere normály a tiež b = 0°). Vtedy sa lúč odráža od povrchu kvapky priamo späť k slnku. Vykonaním vhodnej substitúcie a dosadením do rovnosti (6), dostávame pre uhol dopadu 59,65° minimálny rozptylový uhol pre červenú zložku 137,3° a fialovú 139,2°. Ale dúhu nemôžeme spozorovať s hodnotami rozptylového uhla v rozpätí od 180° do tohoto minima. Preto je nutné nasledujúce vysvetlenie. S ohľadom na rovnosť (1) a využitím Snellovho zákona, dostaneme vzťah:
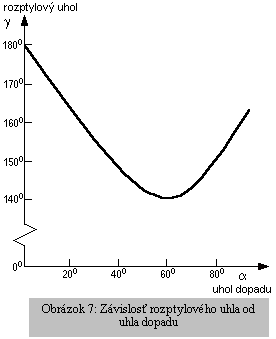
Funkčná závislosť rozptylového
uhla g na uhle dopadu a (Obrázok 7) ukazuje, že pre široký rozsah hodnoty
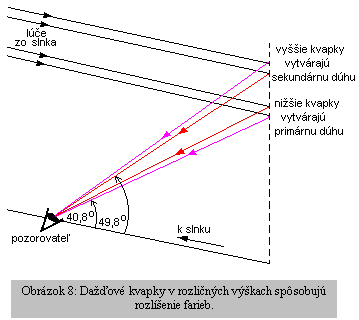
a sa lúče odchyľujú blízko minima rozptylového uhla. Obrázok 8
ukazuje, že tento minimálny rozptylový uhol zapríčiňuje vznik primárnej
dúhy . Fialový kruh v dúhe sa formuje z polkužeľa s uhlom
180° – 139,2° = 40,8° a červený o uhle 42,7° vzhľadom k priamému
slnečnému lúču. Sekundárnu dúhu môžeme
pozorovať na oblohe vyššie než sa nachádza primárna dúha.
Charakterizuje ju opačné radenie farieb ako má primárna dúha (Obrázok 3)
s červenou vo vnútri a fialovou vonku.
Pre minimálny rozptylový uhol (znova má byť rovný nule) teraz dostávame da/db = 3. Analogicky získame vzťah pre uhol dopadu, pri ktorom dochádza k minimálnemu rozptylovému uhlu pre sekundárnu dúhu:
Tieto výsledky spôsobujú,
že fialový kruh v sekundárnej dúhe vzniká z lúčov odchýlených
o uhol 233,6° a červený o uhol 229,8°.
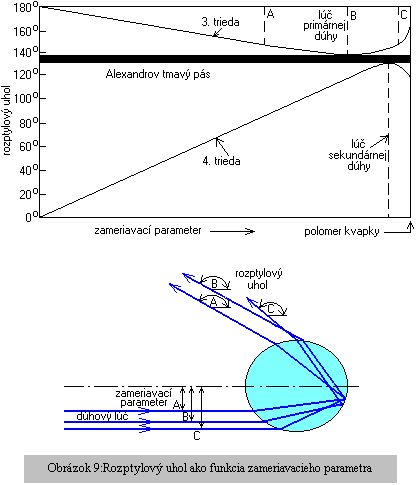
Rozptylový uhol (Obrázok 9) každej triedy rozptylených lúčov sa mení v širokom rozmedzí ako funkcia zameriavacieho parametra. Pretože v slnečnom svetle je kvapka osvetľovaná lúčmi so všetkými hodnotami zameriavacieho parametra súčasne, je svetlo rozptyľované prakticky do všetkých smerov. Prečo je teda v blízkosti uhla pribli6ne 138° intenzita rozptyleného svetla tak zosilnená ? Odpoveď na túto otázku prvýkrát dal Descartes. Aplikoval
zákony odrazu a lomu v každom bode, kde sa lúč stretáva s rozhraním
vzduch – voda a dôkladne vypočítal dráhy mnohých lúčov s rôznymi
hodnotami zameriavacieho parametra. Prvoradý význam majú však lúče 3.
triedy (primárna dúha). Ak je zameriavací parameter rovný nule, je
príslušný lúč rozptýlený pod uhlom 180°, t.j. späť k slnku (Obrázok
9) . Pritom prechádza stredom kvapky a odráža sa od najvzdialenejšieho
bodu jej povrchu. S rastom zameriavacieho parametra sa dopadajúci lúč
vzďaľuje od stredu a uhol rozptylu sa zmenšuje. Descartes však zistil, že
tento trend nepokračuje až do maxima zameriavacieho parametra, kedy sa
dopadajúci lúč dotýka povrchu kvapky ako jeho dotyčnica. Rozptylový uhol
prechádza minimom pri hodnote zameriavacieho parametra zhruba 7/8 polomeru
kvapky a potom opäť rastie. Tento minimálny rozptylový uhol je 138°. U lúčov 4. triedy (sekundárna dúha) je pri nulovom zameriavacom parametre rozptylový uhol rovný nule. Stredový lúč sa dvakrát odráža a potom pokračuje v pôvodnom smere. S rastom zameriavacieho parametra rastie i rozptylový uhol, ale aj tu sa tento trend nakoniec obráti a to tentoraz pri uhle 130°. Lúče 4. triedy majú teda maximálny rozptylový uhol 130° a s ďalším rastom zameriavacieho parametra sa vracajú späť bližšie k dopredu postupujúcemu rozptylovému smeru. Alexandrov
tmavý pás Pri
dôkladnom pozorovaní zistíme, že oblasť medzi oboma oblúkmi je značne
tmavšia než zvyšná časť oblohy. Dokonca aj keď sekundárna dúha nie je
postrehnuteľná, môžeme na okrajoch primárneho oblúka rozoznať svetlejšiu
a tmavšiu „stranu“. Tmavá oblasť dostala názov Alexandrov tmavý pás
podľa gréckeho filozofa Alexandra z Afrodisiady, ktorý ju po prvýkrát
popísal asi r. 200 pred n. l. Keďže kvapka vody je ožiarená slnečným svetlom rovnomerne, je rovnomerné i rozdelenie hodnôt zameriavacieho parametra vstupujúcich lúčov. Sústredenie rozptyleného svetla bude preto najväčšie v tom smere, v ktorom sa rozptylový uhol v závislosti na zameriavacom parametri mení najpomalšie (Obrázok 9). Inými slovami rozptylené svetlo je najintenzívnejšie tam, kde zhrňuje dohromady dopadajúce lúče z najväčšieho intervalu hodnôt zameriavacieho parametra. Oblasti najpomalšej zmeny sú v okolí maximálneho a minimálneho rozptylového uhla. Tým je vysvetlená výnimočnosť charakteristických uhlov primárnej a sekundárnej dúhy. A keďže žiadne z lúčov 3. a 4. triedy sa nerozptyľujú do uhlového sektora medzi 130° a 138°, tak vyniká v tomto uhlovom sektore tmavá oblasť. Tým je z podstatnej časti vysvetlené, prečo vzniká Alexandrov tmavý pás. Nadpočetné
prúžky Len
niekedy pozorovateľným rysom dúhy je rad nezreteľných prúžkov, obvykle
striedavo ružových a zelených. Nachádzajú sa na vnútornej strane primárneho
oblúka a ešte vzácnejšie sa môžu objaviť na vonkajšej strane sekundárneho
oblúka. Tieto nadpočetné prúžky môžeme najlepšie pozorovať blízko
vrcholu oblúka. V tejto uhlovej oblasti vystupujú v rovnakom smere
vždy dva rozptylené lúče 3. triedy. Pochádzajú z dopadajúcich lúčov
s hodnotami zameriavacieho parametra na opačných stranách od hodnoty
odpovedajúcej dúhovému uhlu (Obrázok 9). A tak v ktoromkoľvek danom
smere s uhlom trochu väčším, než je dúhový uhol, obsahuje
rozptylené svetlo dva lúče, ktoré prešli kvapkou dvoma odlišnými
cestami. Tieto lúče vystupujú z povrchu kvapky na dvoch rôznych
miestach, ale ďalej postupujú v rovnakom smere. Tieto dva lúče spolu
interferujú. Keďže rozptylové uhly sú určené rozdielom medzi dĺžkami
dráh týchto lúčov, má na nich vplyv polomer kvapky. Rozloženie
nadpočetných prúžkov preto závisí na veľkosti kvapky. Vo väčších
kvapkách rastie dráhový rozdiel so zameriavacím parametrom oveľa rýchlejšie
ako v malých. A tak čím väčší sú kvapky, tým menší je uhlový
rozostup nadpočetných prúžkov. Zhrnutie Veľkosť
vodných kvapiek má vplyv aj na iné hlavné rysy dúhy. Táto závislosť je
zhrnutá v nasledujúcej tabuľke:
|
|||||||||||||||||
|
Posledná aktualizácia: 09.02.2001
 Daniela Tokárová: TEÓRIA
DÚHY
Daniela Tokárová: TEÓRIA
DÚHY
 Slnečné
svetlo vstupuje do dažďovej kvapky (Obrázok 4) v bode A pod uhlom
dopadu a ( vzhľadom k normále ). Tu sa láme ku kolmici pod uhlom b. Tým
sa odchyľuje od pôvodného smeru o uhol (a - b). Ak lúč svetla dopadne na
povrch kvapky v bode B pod uhlom väčším ako je hraničný uhol, odrazí
sa späť dovnútra kvapky. Keďže je trojuholník AOB rovnoramenný, je uhol
medzi úsečkou AB a normálou v bode B tiež b.
Slnečné
svetlo vstupuje do dažďovej kvapky (Obrázok 4) v bode A pod uhlom
dopadu a ( vzhľadom k normále ). Tu sa láme ku kolmici pod uhlom b. Tým
sa odchyľuje od pôvodného smeru o uhol (a - b). Ak lúč svetla dopadne na
povrch kvapky v bode B pod uhlom väčším ako je hraničný uhol, odrazí
sa späť dovnútra kvapky. Keďže je trojuholník AOB rovnoramenný, je uhol
medzi úsečkou AB a normálou v bode B tiež b.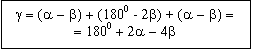 (
1 )
(
1 )