RNDr. Radoslav Kalakay 

Pre fyziku rovnako ako súčasnú vedu a techniku je charakteristické rýchlo narastajúce množstvo poznatkov. Tento problém je ešte znásobený obtiažnou názornosťou pri prezentácii poznatkov modernej fyziky a tak sú kladené značné nároky na schopnosti žiakov nielen akceptovať túto kvantitu učiva, ale aj pochopiť jeho novú kvalitu. Potreba používania názorných prostriedkov vo vyučovacom procese vyplýva predovšetkým z podstaty procesu učenia sa, ktorý sa začína individuálnym poznávacím procesom žiaka.
U starších žiakov (počínajúc druhým stupňom základnej školy, ale najmä na strednej škole) sa poznávací proces často nezačína odvíjať od pozorovania skutočných objektov a javov, prípadne ich obrazov, ale od najrôznejších druhov modelov.  Mnohokrát sa tento proces odvíja aj iným spôsobom napríklad na báze historického prístupu k objavovaniu istého zákona (napr. formulácie prvého zákona termodynamiky), alebo jednoducho od žiakom oznámených vedeckých poznatkov.
Výskumy u nás a v zahraničí ukazujú, že žiaci po absolvovaní kurzov fyziky tradičnou formou majú problémy s chápaním najmä fyzikálnych súvislostí. Narozdiel od „pasívneho poznávacieho štýlu“ aktívne poznávanie kladie väčší dôraz na vlastnú samostatnú poznávaciu činnosť žiakov. Dôraz sa kladie najmä na empirickú skúsenosť a pri učení sa zdôrazňuje použitie reálnych výsledkov experimentov v nadväznosti na teoretické výpočty.
V súvislosti s aktívnym poznávaním sa do žiackych laboratórií dostáva počítač, ako nástroj nielen pre zber dát, ale aj na ich spracovanie a vyhodnotenie. Okrem tohto použitia počítač zohráva dôležitú úlohu aj pri vytváraní matematických modelov fyzikálnych javov. Budovanie a skúmanie matematických modelov je jednou zo základných úloh súčasnej vedy a v súčasnosti tieto modely zohrávajú vo výskume významnú úlohu. Možno preto prirodzene očakávať ich výskyt v zjednodušenej podobe aj v školskej fyzike, kde žiak priamo na vyučovacej hodine má možnosť vytvárať, simulovať a analyzovať fyzikálne javy. Zmenou parametrov môže študovať jeho vlastnosti a skúmať daný jav v rozličných podmienkach.
Počítačových programov umožňujúcich modelovanie s využitím matematických vzťahov je niekoľko, napr. holandský systém IP Coach, obsahujúci podprogram Modelovanie alebo český systém FAMULUS. Spomedzi modelovacích programov ma zaujal portugalský produkt Modellus.

Modellus

Modellus ponúka učiteľom a študentom skúsenosti multiúrovňového učenia sa, v ktorom môžu vytvárať, simulovať a analyzovať modely interaktívnou cestou za použitia počítača, rovnako z experimentánych dát ako aj z teoretických predpokladov. Modelus je softvér pre interaktívne modelovanie s využitím matematiky. Učitelia a študenti môžu použiť Modellus na budovanie modelov a skúmať ich s využitím animácií, grafov a tabuliek.
Namiesto používania algebraických, diferenciálnych a integrálnych rovníc, užívateľ môže experimentovať interaktívne s pripravenými modelmi. Vizualizácia javov pomocou animácií vedie k lepšiemu pochopeniu základných matematických operácii a fyzikálnych javov. Modellus môže byť rovnako použitý ako nástroj na analýzu dát a môže podať zmysel experimentálnym dátam, prípadne je ho možné použiť ako nástroj pre výrobu modelov s využitím grafiky (fotografie, grafy, obrázky atď. v formáte BMP resp. GIF) alebo videí (vo formáte AVI). Modellus môže byť integrovaný aj do základných kurzov matematiky resp. matematickej fyziky či priamo fyziky, alebo vo vyššom kurze spomínaných predmetov na ozrejmenie funkcií, diferenciálnych rovníc či integrálneho počtu.
V priebehu októbra bude dokončená aj slovenská verzia tohto programu. Užívateľ si môže veľmi rýchlo prispôsobiť existujúci model podľa svojich požiadavok. Integritu modelu je možné zachovať zadaním hesla, ktoré ochráni model pred možnými nechcenými zmenami. Modellus dáva učiteľom a študentom silnú technológiu pre štúdium prírodovedných predmetov a matematiky na stredných školách a univerzitách.

Prostredie a požiadavky na hardvér počítača
Modellus, na rozdiel od Famulusu je navrhnutý a naprogramovaný pre prostredie Windows. Programátorský kód je vytvorený v 16 bitovej verzii jazyka C++, preto bez problémov funguje vo Win3.11 alebo Win2000 v počítači s procesorom 486DX a vyššie. Inštalácia programu je pohodlná a intuitívna. K programu sa dodáva aj 107 stranový manuál vo forme pdf súboru, obohatený množstvom obrázkov popisujúcich základy práce s programom, popis predvolených funkcií, popis prostredia a praktické ukážky modelov. Pre ilustráciu uvádzam dva modely z termodynamiky v skrátenej podobe.
Anglickú verziu 2.01 si môžete stiahnuť na tomto mieste Modellus.exe (8,4 MB) aj s ukážkovými modelmi.

 Príklady

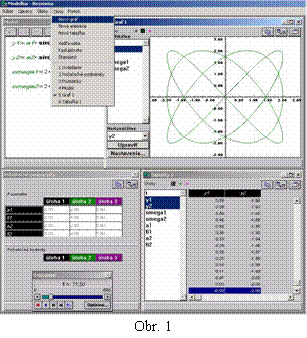
Ak by sme chceli zistiť ako vyzerajú závislosti napr. pre skladanie kmitov rovnakého smeru, vznik rázov, skladanie kmitov na seba kolmých (obr.1), časová závislosť výchylky (ne)tlmeného harmonického oscilátora a iné, museli by sme nakresliť príslušné grafy. Po zmene parametrov, resp. počiatočných hodnôt by sme opätovne museli prekresľovať príslušné grafy. Modellus ponúka výpočet a zobrazenie súčasne piatich úloh, v ktorých si navolíme ľubovoľné počiatočné podmienky. Výstup môže byť grafický alebo tabuľkový s možnosťou exportu do špeciálnych textových editorov resp. tabuľkových procesorov (napr. Excel).

Izotermický dej s ideálnym plynom

Pri izotermickom deji vychádzame z predpokladu, že T₁=T₂. Vzťah medzi tlakom a objemom ideálneho plynu pri izotermickom deji s plynom so stálou hmotnosťou možno zapísať nasledovne: p₁V₁=p₂V₂.

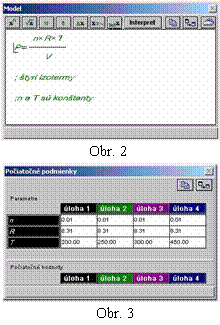
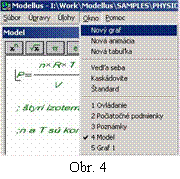
Graf vyjadrujúci závislosť tlaku plynu so stálou hmotnosťou ako funkciu jeho objemu pri izotermickom deji sa volá izoterma. V programe Modellus v časti Model zapíšeme všeobecný tvar stavovej rovnice ideálneho plynu (obr.2). Do automaticky vytvorenej časti počiatočných podmienok a konštánt  zadáme príslušné hodnoty (obr.3). Pre ukážku som navolil štyri hodnoty teploty, pri ktorých budeme sústavu pozorovať. Nasleduje samotné vytvorenie grafu pomocou hlavného menu a funkcie Nový graf (obr.4).

 Po označení súradníc v horizontálnom a vertikálnom smere môžeme kreslenie grafu závislosti tlaku plynu od jeho objemu pri stálej teplote spustiť pomocou tlačidla štart v časti Ovládanie.

Harmonický oscilátor

Príkladom harmonického oscilátora je mechanický pohyb telesa zaveseného na pružine, vychýleného a voľne pusteného.

Na teleso pôsobí v každom okamihu sila F = - kx. Ak okrem tejto sily pôsobí aj sila odporu priamo úmerná rýchlosti pohybu potom pre zrýchlenie oscilátora platí: a = (- kx-bv)/m.

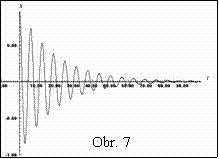
Po vytvorení modelu (obr.6) stačí vytvoriť graf  závislosti x na t. Časová závislosť výchylky tlmeného harmonického oscilátora je na obr.7. Použitím analógií možno vytvoriť matematický model elektromagnetického oscilátora. Stačí nahradiť x→q, v→i, a→di/dt, m→L, k→1/C, b→R.

Program v časti Animácia ponúka navyše funkcie určovania súradníc, merania vzdialenosti medzi dvoma bodmi, merania dráhy, merania plochy pod krivkou, určovania dotyčnice či merania uhla dvoch priamok.

DOWNLOAD
Beta verzia slovenskej lokalizácie: Modellus25BetaSK.exe (400kB) - preložených je 99% programu
Zbierka modelov z konferencie Infovek: Modely.exe (1,12 MB)
Modely v angličtine: advphyst.zip (1,14 MB), Rolland_Fall_1998.zip (140kB), samples_v1.zip (580kB), Veit&Mors.zip (156kB)
Meracie prístorje a pravítka: rulers.zip

Návod: slovenskú verziu rozbaľte do adresára c:\Modellus a spusťte registračné súbory mdl-98-1.reg a mdl-98-2.reg pre verzie windows95, 98, ME

Literatúra:
[1] Kalakay, R.:           Vizualizácia fyzikálnych poznatkov prostredníctvom modelovania. PF UPJŠ Košice, 2001
[2] Teodoro, V. a kol:  Modellus – Workshops and Help. Faculty of Science and Technology, Nova University, Lisbon, Portugal, 2001
[3] Ješková, Z. a kol.:   Počítačom podporovaná výučba fyziky. PF UPJŠ Košice, 2000

RNDr. Radoslav Kalakay, Katedra experimentálnej fyziky, PF UPJŠ v Košiciach, Park Angelinum 9, 04154 Košice, SR – tel. (+421 55) 6221128, e-mail: kalakay@upjs.sk