Obsah
  6.2 Výtok kvapaliny z nádoby - Simulácia  
 

6.3 Energia prúdiacej kvapaliny, Bernoulliho rovnica
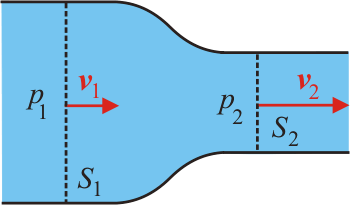Prúdová trubica Vo vodorovnej prúdovej trubici prúdi ideálna kvapalina s hustotou ρ. Rýchlosti ustáleného prúdenia cez prierezy S1 a S2 sú  v1 a v2. Vyjadrite rozdiel  tlakov Δp = p2 – p1v kvapaline medzi uvedenými prierezmi.
Stredy prierezov S1 a S2 vodorovnej prúdovej trubice sú v rovnakej výške h1 = h2  nad zemským povrchom, preto sa tiažová potenciálna energia objemovej jednotky kvapaliny počas prúdenia nemení. Keď pre tieto podmienky použijeme Bernoulliho rovnicu, pre hľadaný tlakový rozdiel dostaneme vzťah:

 
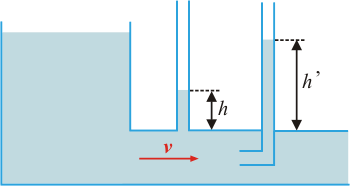
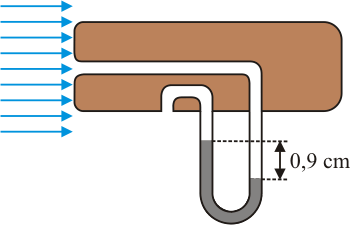
Spôsob merania rýchlosti prúdiacej kvapaliny je založený na platnosti Bernoulliho rovnice. Prvá manometrická rúrka registruje v kvapaline prúdiacej neznámou rýchlosťou v tlak p prostredníctvom výšky h kvapalinového stĺpca. Druhá manometrická rúrka má svoj dolný otvor obrátený proti prúdu kvapaliny. Rýchlosť prúdenia v, v nej klesne na nulu, preto výška h’ kvapalinového stĺpca súvisí s tlakom p´ > p zodpovedajúcim celkovej mechanickej energii kvapaliny na jednotku objemu. Tiažová potenciálna energia je na úrovni dolných otvorov rúrok prakticky rovnaká. Meranie rýchlosti prúdiacej kvapaliny
Podľa Bernoulliho rovnice pre daný prípad platí  vzťah
z ktorého pre hľadanú rýchlosť dostaneme
   
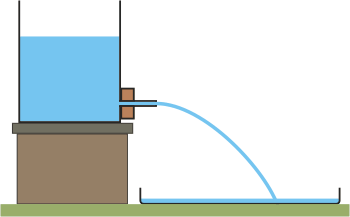
Odvoďte vzťah pre veľkosť rýchlosti v, ktorou by mala vytekať dokonalá kvapalina malým otvorom v stene nádoby, nachádzajúcom sa v hĺbke h pod voľným povrchom kvapaliny. Rýchlosť poklesu hladiny v nádobe v porovnaní s výtokovou rýchlosťou považujte za zanedbateľnú. Atmosferický tlak v okolí nádoby má hodnotu pa.

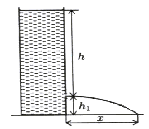
pozri súvisiaci demonštračný experiment - video/animáciu 		Vytekanie kvapaliny z nadoby 
V Bernoulliho rovnici zapísanej pre mechanickú energiu objemovej jednotky kvapaliny v mieste voľného povrchu a v otvore, ktorým kvapalina vyteká, zavedieme označenie
h1 = h, 
v1 = 0 m.s-1,
p1 = p,
h2 = 0 m,
v2 = v = ?m.s-1, 
p2 = p
a získame rovnicu 		 Vytekanie kvapaliny z nadoby
z ktorej pre výtokovú rýchlosť dostávame Torricelliho vzťah
Práve takúto rýchlosť by získali častice kvapaliny pri voľnom páde z výšky h.
  1. Pri akých podmienkach má kvapalina tlakovú potenciálnu energiu?
  2. Odvoďte vzťah na určenie tlakovej potenciálnej energie kvapaliny s objemom ΔV a tlakom p.
  3. Napíšte Bernoulliho rovnicu a vysvetlite fyzikálny význam jednotlivých členov v tejto rovnici.
  4. Ako sa mení tlak a rýchlosť prúdenia kvapaliny v potrubí s premenlivým prierezom?
  5. Voda prúdi vodorovným potrubím s priemerom 4 cm rýchlosťou 1,2 m.s-1. Potrubie sa zužuje na priemer 2,4 cm. Vypočítajte zmenu tlaku vody v potrubí v zúženom mieste, vzhľadom na tlak vody v nezúženom priereze.    [1,28 kPa]
  1. Vypočítajte koľkokrát sa zmenší tlak prúdiacej kvapaliny, ak sa jej rýchlosť v zúženom priereze vzhľadom na rýchlosť prúdenia v širšom priereze zdvojnásobí. [4 krát]
  2. V Prandtlovej trubici (obrázok) používanej na meranie rýchlosti lietadla je použitá ortuť. Rozdiel hladín stĺpcov ortuti je 0,9 cm. Letí lietadlo nadzvukovou rýchlosťou?     [Nie, rýchlosť je asi 129,6 km.h-1]
  3. Voda vyteká z otvorenej nádoby rýchlosťou 0,5 m.s-1. Vypočítajte v akej výške nad otvorom je voľná hladina. Predpokladajte, že voda je dokonalou kvapalinou.     [1,25 cm]
Prandtlova trubica
   
6.2 Výtok kvapaliny z nádoby - Simulácia
Obsah