Obsah

  
  4.3 Paradox vztlaku 5. Ustálené prúdenie tekutiny    
 

4.4 Vztlaková sila, Hydrostatická vztlaková sila, Archimedov zákon

  
 
Hmotnosť vzduchu v triede s rozmermi 8m X 6m X 3,5m je väčšia ako 220 kg. Uniesli by ste toto množstvo vzduchu, keby sa Vám ho podarilo prečerpať do ľahkého obalu s hmotnosťou asi 10 kg a keby objem ostal rovnaký?  
Uniesli, lebo by ste niesli len tiaž obalu. Vztlaková sila vonkajšej atmosféry by bola rovnaká ako tiaž vzduchu vo vnútri obalu.  
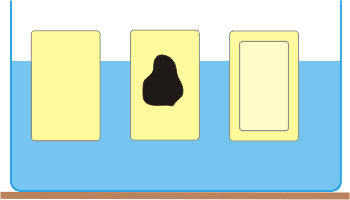
V nádobe s vodou pláva kúsok ľadu, ktorý: Nádoba s ľadom kameňom a vzduchom  
  1. je rovnorodý
  2. obsahuje zamrznutý kamienok
  3. obsahuje zamrznutú vzduchovú bublinu.

Rozhodnite, či sa zväčší, zmenší alebo nezmení výška hladiny vody nad dnom nádoby, keď sa ľad roztopí.

  
  1. Ak je ľad rovnorodý, potom tiaž vody, ktorá je vytlačená ponorenou časťou je rovnaká, ako tiaž celého kusu ľadu, teda aj vody, ktorá z ľadu vznikne po rozpustení. Preto sa výška povrchu hladiny nezmení.
  2. Ľad so zamrznutým kameňom vytlačí viac vody, ako zodpovedá objemu samotného ľadu a objemu samotného kameňa, pretože hustota kameňa je väčšia ako hustota vody a priemerná hustota uvažovanej sústavy: kameň + ľad  je menšia ako hustota vody.  V tomto  prípade po roztopení ľadu hladina klesne.
  3. Ak je v ľade vzduchová bublina, je jej účinok rovnaký ako keby zo spodku pôsobil na ľad o rovnakej tiaži balónik naplnený vzduchom rovnakého objemu ako má bublina. Objem časti ľadu pod hladinou ponoru je menší ako objem, ktorý by zodpovedal ponorenej časti rovnorodého ľadu. Ak sa ľad roztopí, hladina stúpne (prípad ak je vzduchová bublina pod čiarou ponoru). V opačnom prípade je účinok rovnaký, ako keby sme nadľahčovali ľad smerom hore silou, ktorá sa rovná vztlakovej sile vzduchovej bubliny vo vode. Hladina však opäť stúpne.
  
 
Vypočítajte veľkosť vztlakovej sily, ktorou je nadľahčované železné teleso s hmotnosťou 100 g a hustotou 7800 kg.m-3 pri úplnom ponorení do vody. Hustota vody je 1000 kg.m-3. Určte aj veľkosť výslednej sily F pôsobiacej na teleso ponorené v kvapaline.  
 
mt = 100 g = 0,100 kg
 ρt = 7800 kg.m-3
ρk = 1000 kg.m-3
Vk = Vt = mt / rt
 g = 10 m.s-2		 Tiažová sila FG = mg pôsobiaca na teleso má veľkosť
FG = 0,100 kg .10 m.s-2 =  1,0 N.		  
 
Hydrostatická vztlaková sila
Fvz = Vk ρk g =(mt / ρt)ρkg =(mtρk/ρt)g
pôsobiaca na teleso zvisle nahor (vztlaková sila teleso nadľahčuje) má veľkosť
Fvz = (0,100 kg. 103 kg.m-3 / 7,8. 103 kg.m-3).10 m.s-2
 Fvz = 0,128 N.		  
 
Veľkosť výslednej sily Fv = FG + Fvz namierenej zvisle nadol je približne Fv = Fvz - FG = 1,0 N - 0,128 N = 0,87 N
Na rôznych miestach Zeme je tiažové zrýchlenie rôzne. Má zmena tiažového zrýchlenia na ponor lode?  
Nemá. Podľa Archimedovho zákona sa tiaž plávajúcej lode rovná tiaži vody, ktorá má rovnaký objem ako jej ponorená časť.  Ak sa zmení tiažové zrýchlenie, zmení sa v rovnakom pomere tiaž lode i tiaž príslušného objemu vody.  
   
Ak je teleso úplne ponorené v kvapaline, ktorá má rovnakú hustotu ako je hustota telesa, tak je tiaž vyrovnaná vztlakovou silou a teleso sa vznáša. Môžeme sa teda domnievať, že teleso je v beztiažovom stave?  
Nie. Beztiažový stav je charakterizovaný tak, že chýba vonkajšie silové pole. Ale v našom prípade existuje tiažové pole a všetky javy s ním súvisiace.  
   
Platí Archimedov zákon v beztiažovom stave, napr. na kozmickej lodi?  
V beztiažovom stave Archimedov zákon neplatí. Na teleso vo vnútri kvapaliny nepôsobí vztlaková sila, pretože rozdiel tlakov na dolnú a hornú základňu je nulový.  
 
  1. Vysvetlite, ako vzniká hydrostatická, alebo aerodynamická vztlaková sila a vyvoďte vzťah pre jej určenie.
  2. Ktoré podmienky sú splnené, pokiaľ teleso ponorené do kvapaliny v nádobe:
    1. klesne na dno,
    2. pláva čiastočne ponorené,
    3. voľne pláva v ľubovoľnej hĺbke pod hladinou.
  3. Vyslovte Archimedov zákon a vysvetlite jeho fyzikálny obsah.
  4. Rozhodnite, či vztlaková sila vzniká aj v beztiažovom stave. Svoje tvrdenie fyzikálne zdôvodnite.
  5. Vysvetlite:Loď
    1. prečo sa loď zhotovená z veľkej časti  z ocele nepotopí,
    2. aký vplyv na ponor nákladnej lode má hmotnosť jej nákladu.
  
  1. Pri vyberaní kameňa z vody sme pôsobili silou 120 N. Akou veľkou silou budeme musieť pôsobiť, ak budeme kameň premiestňovať nad vodnou hladinou? Hustota kameňa je 5000 kg.m-3. [150 N]
  2. Aký objem vody vytlačila sklená fľaša s hmotnosťou 0,5 kg plávajúca na vode? [50 cm3]
  3. Aké najťažšie teliesko unesie pohár plávajúci na vodnej hladine, keď jeho vonkajší objem je 200 ml a má hmotnosť 10 g? [190g]
  4. Akou časťou svojho objemu je ponorená ľadová kryha v morskej vode s  hustotou 1030 kg.m-3, ak hustota ľadu je 900 kg.m-3?  [Asi 87%]
  5. Zdôvodnite vznášanie sa vzducholode v rôznych výškach nad zemským povrchom.
 Fľaša na vode  
Vzducholoď  
 
4.3 Paradox vztlaku 5. Ustálené prúdenie tekutiny  
Obsah