 Obsah
Obsah
Harmonický Oscilátor (Perióda - Hmotnosť - Pružnosť)
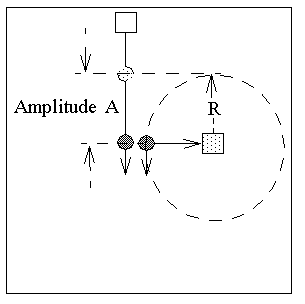
Táto simulácia demonštruje existenciu analógie medzi pohybom harmonického oscilátora a rovnomerným kruhovým pohybom.Pohyb harmonického oscilátora môžeme definovať ako lineárnu projekciu rovnomerného kruhového pohybu.
|
Pre rovnomerný kruhový pohyb máme:
Perióda T = 2 π R / v
Ako dostredivú silu máme:
fd = m v2 / R
Pretože oba objekty majú v ľubovoľnom časovom okamihu rovnakú zvislú polohu,
sily pôsobiace v kolmom smere, musia byť rovnaké v ľubovoľnom časovom okamihu.
Preto máme pre najvyššiu alebo najnižšiu polohu:
fd = fmax = D A
Pri R = A dostaneme substitúciou a úpravou:
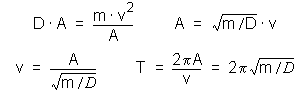
To dokazuje v súlade so simuláciou na predchádzajúcej strane vzťah:
T ~ √ (m/D).
Čas T potrebný pre jednu periódu je nezávislý na rýchlosti, pri ktorej sa
objekt vychýli z rovnovážnej polohy.
