 Obsah
Obsah
Rýchlosť na kruhovej obežnej dráhe ako funkcia polomeru r
Úlohy podobné poslednej môžu byť vyriešené oveľa efektívnejšie pomocou výpočtu. Aby ste to urobili
musí byť známe aká sila pôsobí a aké bude výsledné zrýchlenie, ak sa má dať objekt pohybovať po
kruhu. Táto pôsobiaca sila fc sa nazýva dostredivá sila, čo znamená že je orientovaná do stredu. Zrýchlenie sa nazýva radiálne zrýchlenie pretože je orientované v smere polomeru kruhovej obežnej dráhy.
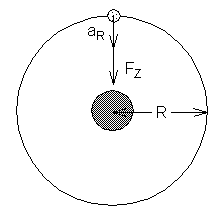 |
Ako vždy v mechanike fc
a aR spĺňajú Newtonov základný zákon: fc=m*aR. Pre vzťah medzi radiálnym zrýchlením aR, dráhovou rýchlosťou v a polomero obežnej dráhý R máme: aR=v2/R. Pre dostredivú silu z toho vyplýva:  |
Gravitačná sila je daná všeobecným zákonom gravitácie:
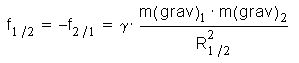
Pri pôsobení na satelit, v okolí centrálneho objektu dostaneme:
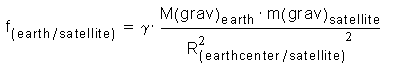
Pri tom sa odvolávame na fakt, že guľové teleso (ako Zem) sa chová navonok akoby všetka jeho
hmotnosť bola sústredená v jeho strede.
Preto musíme vzdialenosť brať od stredu centrálneho telesa.
Pretože dostredivá sila, potrebná pre kruhovú obežnú dráhu je realizovaná
pomocou tejto gravitačnej sily dostaneme:
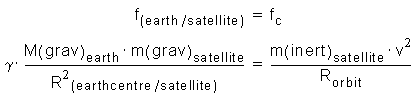
Zo skutočnosti že zotrvačná a gravitačná hmotnosť sú si úmerné a merateľné
v rovnakých jednotkách vyplýva:

S R(stred centrálny objekt/satelit)=R(obežná dráha) a riešením pre v dostávame:

Ak rýchlosť v1 a polomer R1 pre špecifické obežné dráhy sú známe a ak rýchlosť v2 pre rozdielné polomery R2 je potrebne vypočítať, máme: v1/v2 = √(R2/R1).
Príklad: Z R2/R1 = 2 vyplýva: v2 = v1 / √2.
