 Obsah
Obsah
Kruhový pohyb založený na elastickej interakcii - Výpočet
V predchádzajúcej simuláicii boli dva objekty rovnakej hmotnosti spojené elastickou pružinou a pohybovali sa na spoločnej kruhovej dráhe. Na dosiahnutie tejto situácie, pružinou aplikovaná sila na oboch koncoch, musí korešpondovať s dostredivou silou, ktorá je nevyhnutá k udržaniu každého objektu na kruhovej dráhe. Pôsobiacu sila od napnutej pružiny môžeme vypočítať na základe Hookovho zákona.fpružina = s D
(l0 = dĺžka v pokoji; l = skutočná dĺžka pod napätím; s = l - l0; D = tuhosť pružiny)
K dosiahnutiu kruhovej dráhy sa musí zhodovať sila pružiny s dostredivou silou f = m v2/R ktorá je potrebná pre časticu hmotnosti m na pohyb s rýchlosťou |v| na kruhovej dráhe s polomerom R.
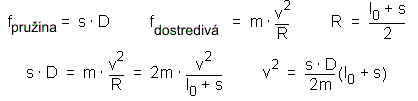
Parametre pre danú simuláciu sú (v zodpovedajúcich jednotkách): l0; = 1500; s = 100; m = 2; D = 1;
Tieto hodnoty dovoľujú vypočítať rýchlosť a porovnať ju s hodnotou zo simulácie.
Pre m ≠ 2 rovnica vyššie už neplatí. Obežná dráha sa viac alebo menej odchyľuje od kruhovej dráhy.
