Obsah

Šikmý vrh - Simulácia

Zmenou vodorovne a kolme orientovaných zložiek počiatočnej rýchlosti skúste zasiahnuť "kôš", ale pokiaľ je to možné zhora, bez zasiahnutia "stropu".

Počiatočná rýchlosť lopty v smere osi x

vx = jednotiek
Zvýšenie vx o Δv = +10, +100 -10, -100 jednotiek

Počiatočná rýchlosť lopty v smere osi z
vz = jednotiek
Zvýšenie vz o Δv = +10, +100 -10, -100 jednotiek

Rozumnou alternatívou k metóde pokusu a omylu je metóda založená na teórii.

Numerické riešenie

K numerickému riešeniu problému predstaveného na videu, sú potrebné nasledujúce vzťahy, ktorým musíme porozumieť:
Pre pohyb s konštantným zrýchlením: s = 1/2 g t2; v = g t;
(s = prejdená vzdialenosť (dráha); v = rýchlosť; g = tiažové zrýchlenie; t = časové rozpätie)
Pre pohyb s konštantnou rýchlosťou: s = v t.

Z princípu superpozície vyplýva, že pohyb zobrazený na videu a simulácii môžeme rozložiť na dve časti, zvislý vrh s konštantným zrýchlením a vodorovný pohyb s konštantnou rýchlosťou.
Pre dve zložky zvislého vrhu s rýchlosťou stúpajúcou a klesajúcou platí:



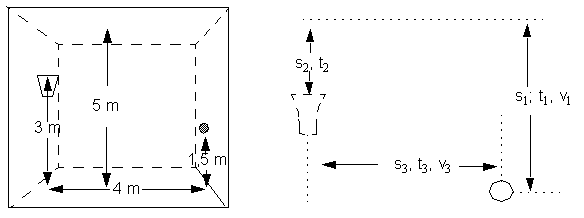
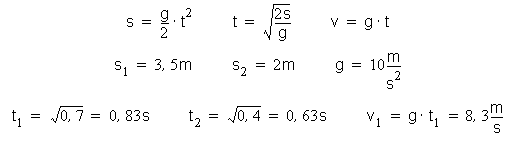
Pre vodorovný pohyb platí:


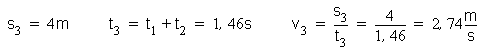
Hodnoty platné pre simuláciu sú: s1 = 1250 jednotiek; s2 = 450 jednotiek; s3 = 1600 jednotiek; g = -100 jednotiek.

Platí tu zhoda medzi numerickým riešením a simuláciou?

Obsah Dlhá tyč a padajúca lopta - Experiment