|
 Teda pri funkciách, ktoré niekedy rastú a niekedy klesajú, nemožno
podľa druhého čísla usporiadanej dvojice (funkcie) vždy jednoznačne
určiť prvú hodnotu.
Tak to bolo aj pri výške stĺpiku vody, keď voda mohla mať 2 alebo 6
stupňov Celzia. Takéto funkcie nie sú prosté. Teda pri funkciách, ktoré niekedy rastú a niekedy klesajú, nemožno
podľa druhého čísla usporiadanej dvojice (funkcie) vždy jednoznačne
určiť prvú hodnotu.
Tak to bolo aj pri výške stĺpiku vody, keď voda mohla mať 2 alebo 6
stupňov Celzia. Takéto funkcie nie sú prosté.
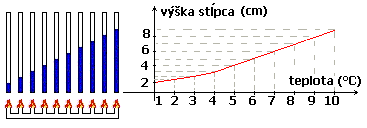  Keby sme sledovali rozpínanie napr. liehu, tak každej výške
stĺpčeka v rúrke prislúcha len jediná možná teplota, pri ktorej lieh
vystúpil do tejto výšky. Takéto funkcie (pri ktorých vieme vždy
jednoznačne z výšky stĺpčeka určiť teplotu kvapaliny v ňom) nazývame
v matematike prosté funkcie. Keby sme sledovali rozpínanie napr. liehu, tak každej výške
stĺpčeka v rúrke prislúcha len jediná možná teplota, pri ktorej lieh
vystúpil do tejto výšky. Takéto funkcie (pri ktorých vieme vždy
jednoznačne z výšky stĺpčeka určiť teplotu kvapaliny v ňom) nazývame
v matematike prosté funkcie.
|

