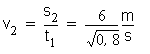Obsah
Obsah
Vodorovný vrh - Numerické riešenie
K vyriešeniu problému predloženého na predchádzajúcej strane, sú potrebné nasledujúce vzťahy, ktorým je potrebné porozumieť:Pre pohyb s konštantným zrýchlením: s = 1/2 a t2; v = g t;
(s = prejdená vzdialenosť (dráha); v = rýchlosť; a = zrýchlenie; t = časový interval)
Pre pohyb s konštantnou rýchlosťou: s = v t.
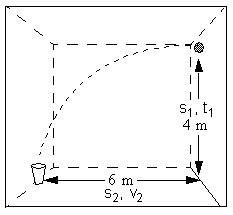
Z princípu superpozície vyplýva, že pohyb zobrazený na videu a v simulácii môžeme rozložiť do dvoch častí, voľného pádu s konštantným zrýchlením a = g a vodorovného pohybu s konštantnou rýchlosťou v.
|
|
Pre voľný pád v kolmom smer máme: 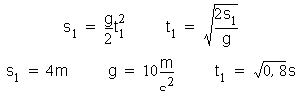
Pre vodorovný pohyb máme:
|
Platí tu zhoda medzi teóriou a simuláciou?