Obsah
  3.6 Hydrostatický tlak - príklady, otázky, úlohy 4.1 Archimedov zákon  
 

4. Hydrostatická vztlaková sila
Človeku prirodzeným prostredím je Zem a vzduch, s tým súvisí jeho pohyb po súši. Avšak človek sa dokáže pohybovať aj vo vode a pod vodou, ktorá je domovským prostredím rýb. Človek sa naučí plávať vo vode, naučí sa potápať. Zvieratá, ktoré sa rodia vo vode vedia prirodzene plávať, niektoré suchozemské zvieratá aj keď sa narodia na súši ako človek sa nemusia učiť plávať, vedia to už od narodenia.
Kačičky Tučniak Pes Kôň
Človek a ryba Žralok
zdroj: pozri zoznam zdrojov
 
Človek, aby si uľahčil pohyb po vode a pod vodou vymyslel dopravné prostriedky ako sú lode, ponorky. Pri týchto dopravných prostriedkoch využíva hydrostatickú vztlakovú silu a platnosť Archimedovho zákona.
 
Loď Tanker Lietadlová loď Lietadlová loď a loď červeného kríža
Ponorka Ponorka Nukleárna ponorka
zdroj: pozri zoznam zdrojov
 
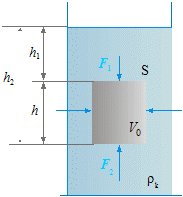
Tlaková sila vyvolaná vlastnou tiažou kvapaliny pôsobí (rovnako, ako tlaková sila vyvolaná ľubovoľnou vonkajšou silou) na všetky strany, teda aj smerom nahor. Na obrázku je znázornený zvislý valec s podstavou s obsahom S ponorený celým svojim objemom V0 do kvapaliny s hustotou rk. Jeho horná podstava je v hĺbke h1 a dolná podstava v hĺbke h2 pod voľnou hladinou kvapaliny.
Z predchádzajúcej state vieme, že s rastúcou hĺbkou v kvapaline rastie aj hydrostatický tlak. V horizontálnom smere pôsobia na plášť valca v rovnakej hĺbke zo všetkých strán rovnako veľké tlakové sily, preto je výsledná sila pôsobiaca na ponorené teleso v horizontálnom smere nulová.		 Valec v kvapaline

Na hornú podstavu pôsobí kvapalina tlakovou silou F1. Jej veľkosť je F1 = h1rgS a pôsobí zvisle nadol, na dolnú podstavu  silou F2. Veľkosť F2 = h2rgS > F1 v smere zvisle nahor.
Výslednica týchto síl Fvz = F1+ F2  pôsobiaca na valec zvisle nahor sa nazýva hydrostatická vztlaková sila.
Jej veľkosť určíme zo vzťahu: 
FVZ = F2 – F1 

FVZ = (h2 – h1)ρkgS            FVZ = hSρkg

FVZ = Vρkg 
kde h = h2 – h1 je výška valca a V = hS je objem ponoreného valca. 
 
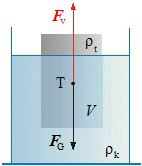
Ak teleso nie je v kvapaline ponorené úplne, objem V ponorenej časti telesa je menší, ako objem V0 celého telesa. 

Veľkosť hydrostatickej vztlakovej sily nezávisí od tvaru ponorenej časti telesa ani od hĺbky, v ktorej je teleso ponorené. Pôsobisko hydrostatickej vztlakovej sily je v ťažisku telesom vytlačeného kvapalinového telesa.

 Súčin Vρk sa rovná hmotnosti mk kvapaliny s rovnakým objemom Vk = V, ako má ponorená časť telesa. Vztlaková sila Fvz = Vkρkg  má preto veľkosť tiaže Gk = mkg kvapaliny vytlačenej ponorenou časťou telesa. Túto skutočnosť si uvedomil už Archimedes v 3. storočí p.n.l.

Čiastočne ponorené teleso 
 
3.6 Hydrostatický tlak - príklady, otázky, úlohy  4.1 Archimedov zákon  
Obsah