|
Sila a základný zákon
mechaniky
Hermann Härtel
Marián Kireš, Zuzana Ješková, Ján Degro
3. O sile
3.1 Vlastnosti sily
Od čias Aristotela, teda viac než 200 rokov, bola sila považovaná za príčinu
pohybu. Až Newton v 17. storočí objavil, že teleso pohybujúce sa rovnomerne,
konštantnou rýchlosťou, nepotrebuje silu.
Silu potrebujeme iba vtedy, ak chceme zmeniť
veľkosť rýchlosti
resp. jej smer, teda iba ak sa teleso pohybuje zrýchlene.
Aj vtedy, keď sa teleso pohybuje konštantnou rýchlosťou (zrýchlenie sa
rovná nule), môžu na teleso pôsobiť rôzne sily. Všetky tieto sily sú však v
rovnováhe a ich výslednica sa rovná nule.
Newton tiež zistil, že nie je jednoduché vytvoriť jednu samostatnú silu. Ak na
seba pôsobia dva objekty, sily sa vždy vyskytujú v pároch. Tieto sily sú
rovnaké čo do veľkosti, ale pôsobia opačným smerom. Tento fakt je známy ako
akcia a reakcia.
3.2 Sila ako vektor
Sily patria k fyzikálnym veličinám, ktoré majú veľkosť aj smer. Takéto
veličiny sa volajú vektory. Vektory sú tiež napr. rýchlosť a
zrýchlenie.
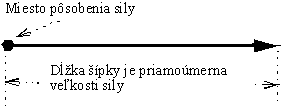
 3.3 Skladanie síl 3.3 Skladanie síl
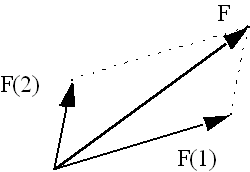
Vektorové veličiny možno skladať. Dve sily môžeme nahradiť jednou výslednou
silou, ktorá má rovnaký účinok ako dve jednotlivé sily. Pri takomto skladaní
sa používa obyčajne grafická metóda, ktorá je ukázaná na nasledujúcom obrázku.
Výslednica dvoch síl F(1) a F(2) je rovná sile
F. Táto sila F tvorí uhlopriečku rovnobežníka so
stranami F(1) a F(2). Veľkosť uhlopriečky určuje
veľkosť sily F.
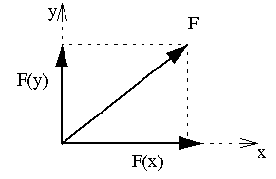
Opačný proces k skladaniu je rozklad síl. Sila môže byť rozložená na dve
alebo viac zložiek. Účinok sily F môže byť nahradený napr. jej
dvomi zložkami orientovanými v smere x a y. Pre takýto rozklad sa používa
rovnaká metóda rovnobežníka.
Pretože x a y sú navzájom kolmé, rovnobežník prechádza na obdĺžnik.
3.4 Jednotka sily
Jednotka pre meranie sily sa volá Newton, skratka N.
Jednotka Newton však nie je základná jednotka, ale odvodená.
Jej súvis so základnými jednotkami (m, kg, s) je prostredníctvom Newtonovho
zákona mechaniky:
F = m.a
1 N = 1 kg.m.s-2
3.5 Meranie jednotiek a simulácie
Keď vykonávame reálne experimenty, musíme definovať jednotky, ktoré budeme
používať. Keď robíme experimenty pomocou počítačových similácii, experimenty
sú vykonávané vo virtuálnom svete, kde používanie jednotiek ako meter by boli
umelé. Vzdialenosti medzi objektami na obrazovke nemôžu byť v metroch.
Jednotky preto vyberieme voľne a pomenujeme ich. Kvôli nedostatku priestoru na
obrazovke budú názvy jednotiek schované. Avšak keď budeme robiť výpočty, tieto
jednotky musíme uvažovať.
4. Základný zákon mechaniky
4.1 Definícia
Základný zákon mechaniky objavený Newtonom v 17. storočí popisuje vzťah medzi
výslednicou síl pôsobiacou na teleso a jeho zrýchlením, ktoré táto sila
spôsobuje.
Tento zákon možno vyjadriť v matematickej forme nasledovne:
F = m.a
kde: F = sila; m = hmotnosť; a = zrýchlenie
Slovami:
Ak výslednica síl (súčet viacerých síl) pôsobí na teleso, toto teleso sa bude
pohybovať so zrýchlením a. Hmotnosť telesa m sa niekedy nazýva
zotrvačná hmotnosť. Charakterizuje, v akom rozsahu sa bude meniť zrýchlenie
pod vplyvom tejto výslednej sily. Čím väčšia zotrvačná hmotnosť, tým menšie
zrýchlenie pri danej sile a naopak.
Príklady
Auto sa pohybuje po diaľnici konštantnou rýchlosťou. Na auto pôsobia rôzne
sily: ťažná sila motora, odpor vzduchu, trenie, tiaž a reakcia cesty, ktorá
kompenzuje tiaž. Pretože sa rýchlosť auta nemení, môžeme povedať, že všetky
sily sú v rovnováhe, teda výslednica síl sa rovná nule.
Lietadlo pristáva a všetky prístroje ukazujú, že jeho rýchlosť je konštantná.
Na pristávajúce lietadlo pôsobí tiažová sila, vztlaková sila, trecia sila,
ktoré nepoznáme. Pretože je rýchlosť lietadla konštantná, výslednica síl sa
musí rovnať nule.
Plavec pláva v bazéne. Ak sa jeho telo pohybuje konštantnou rýchlosťou
(zanedbávajúc pohyb rúk a nôh), môžeme povedať, že výslednica síl pôsobiacich
na plavca sa rovná nule.
 | 