Uvažovali ste už niekedy, prečo sa kužeľosečky volajú práve kužeľosečky ? Dôvod je jednoduchý. Všetky známe kužeľosečky ( matematik by povedal regulárne kužeľosečky ) totiž možno vyrobiť zrezávaním kužeľa. Predstavte si dva kužele spojené vo vrchole, ktoré sú nekonečné. Ak budeme kužeľ rezať rovinou kolmou na os kužeľa, dostaneme kružnicu. Keď túto rovinu trošku nakloníme, rezom bude elipsa. Pri ďalšom nakláňaní roviny sa nám rez náhle "otvorí", dostali sme parabolu. Stačí len malé vychýlenie roviny a rez bude dvojdielny, pretože rovina v tejto polohe pretne obidva kužele. Rezom je tentoraz hyperbola.
        Samozrejme existuje aj iný model-baterkový. Keď si posvietime baterkou rovno dolu, na zemi sa objaví kruh. Po malom vychýlení sa kruh natiahne a vytvorí elipsu. Akonáhle bude svetelný lúč baterky rovnobežný so zemou, uvidíme parabolu. Pri ďalšom nadvihnutí baterky sa na zemi objaví svetelná stopa ohraničená hyperbolou.

Po elipsu či kružnicu dokonca stačí zájsť do najbližšej chladničky! Vyberme si napríklad nejakú salámu a pokúsme na narezať zopár plátkov. Ak krájame kolmé rezy, získame okrúhle plátky, plátky s kruhovou plochou. Šikmým rezom získame podlhovasté plátky, ktoré, napriek tomu, že sme krájali z tej istej salámy, sú väčšie než kruh. Čiaru, ktorá ich ohraničuje nazývame elipsou.

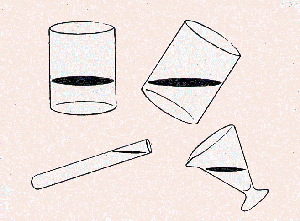
S elipsou sa stretneme pri mnohých iných príležitostiach. Vezmite pohár a naplňte ho asi do  polovice vodou. Ak pohár stojí na stole, hladina  tvorí kruh. Keď pohár trošku nakloníte, z kružnice sa stane elipsa. Ak použijete na pozorovanie veľmi   úzku nádobu, napríklad laboratórnu skúmavku,  uvidíte, že existujú i veľmi úzke elipsy.          Elipsy vidíme veľmi často. Vlastne vždy, keď   sa na kružnicu dívame šikmo. Všimnite si pri najbližšej príležitosti tanier na vedľajšom stole, alebo pozorujte niekedy cyklistu ( prípadne cyklistku ) z okna.