Podrobný výklad,
alebo POHYB TELESA V SILOVOM POLI ZEME
Pri pohybe telesa v zemskom silovom poli pôsobia na teleso viaceré sily: Gravitačná, ktorá sa prejavuje medzi dvoma telesami ako vzájomná príťažlivá sila; Odstredivá, ktorá v dávnych časoch, keď bola Zem ešte tvarovateľná, spôsobila jej sploštenie; Coriolisova sila, o ktorej si teraz niečo povieme a mnoho iných, ako odporová atď.
Príčinou Coriolisovej sily je otáčanie Zeme.
Coriolisova sila je nenulová len vtedy, ak je teleso vzhľadom na zemský povrch v relatívnom pohybe.
Najväčšiu hodnotu dosiahne Coriolisova sila vtedy, ak je smer rýchlosti telesa kolmý na zemskú os.
Za relatívneho pokoja sa Coriolisova sila rovná nule.
Coriolisova sila napríklad spôsobuje, že telesá pohybujúce sa na vodorovnej rovine si nezachovávajú
smer svojho pohybu. Ten sa na severnej pologuli stáča vpravo, na južnej vľavo (napríklad pasátne vetry;
rieky - tie vymieľajú na severnej pologuli viac svoje pravé brehy). Coriolisova sila je príčinou aj
toho, že, okrem na póloch, nepadajú telesá zvislo na zem, ale sa od zvislého smeru odchyľujú
na východ.Coriolisova sila sa prejavuje aj tým, že rovina matematického kyvadla na severnej pologuli sa vzhľadom na smer okamžitého pohybu kyvadla stáča vždy vpravo, teda v zmysle pohybu hodinových ručičiek.
Coriolisova sila je zotrvačná sila, ktorá vzniká v otáčajúcej sa sústave z pohľadu pozorovateľa s ňou
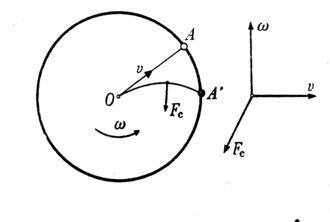
spojeného.Ak v strede dosky O, ktorá je v kľude, udelíme guličke rýchlosť v, pohybuje sa priamočiaro v smere OA. Ak sa doska otáča, prebieha pohyb pozorovaný zvonku rovnako ako predtým (trenie zanedbávame). Gulička sa pohybuje podľa myslenej priamky OA. Na doske sú to však iné body, po ktorých sa gulička pohybuje. Teda pre pozorovateľa na doske opisuje gulička zakrivenú dráhu OA’, pričom AA’ je oblúk, o ktorý sa doska pootočí počas trvania pohybu guličky v smere OA.
Výraz pre Coriolisovu silu odvodíme hneď pre prípad, že bod, z ktorého je vrhnuté teleso, nie je položený v strede dosky O, ale v ľubovoľnom bode P. Uvažujme, že polomer dosky je R, doska sa otáča uhlovou rýchlosťou ω. Vzdialenosť bodu P od osi otáčania je ρ.
Teleso je z bodu P vrhnuté
rýchlosťou v. Otáčavú dosku si myslene ohraničme valcovou stenou, ktorá sa s doskou neotáča.
Keby bola doska v kľude, (ω = 0), guľka by dopadla do bodu A. Aby vrhnuté teleso vykonalo
dráhu PA=R - ρ,
potrebuje na to čas τ = (R - ρ)/v. Pretože sa doska otáča, bude
pozorovateľ po tomto čase τ v bode P’. Ak
nevie nič o otáčaní, očakáva dopad telesa v bode B. Následkom otáčania okolo O má guľka aj
rýchlosť u = ωρ , ktorá je kolmá na spojnicu OP. Guľka teda opustí
miesto P výslednou rýchlosťou,
ktorá vznikne zložením rýchlostí u a v. Pohybuje sa po priamke PC a na stenu dopadne v bode C.Vzdialenosť bodu C od A sa rovná dráhe, ktorú by gulička vykonala za dobu τ len rýchlosťou u. Teda oblúk AC = uτ = u(R - ρ)/v = ωρ(R-ρ)/v.
Pozorovateľ, ktorý vidí vrhnutú guľku dopadnúť v bode C namiesto v očakávanom bode B, usudzuje, že na guľku musí pôsobiť ešte nejaká sila kolmo na smer rýchlosti v, ktorá odchýli guličku o oblúk BC.
BC=AB-AC=Rφ-uτ=Rωτ-ρωτ=(R-ρ)ωτ= ((R-ρ)/v)vωτ=vωτ2
Ak predpokladáme, že veľkosť sily je stála, je stála aj veľkosť príslušného zrýchlenia a teda odchýlka od radiálneho smeru BC = s = (a/2)τ2 .
Z porovnania posledných dvoch rovníc vyplýva: vωτ2 = (a/2)τ2 => a = 2vω .
Zo známeho zrýchlenia dostávame pre príslušnú silu vzťah
Z pohľadu pozorovateľa, ktorý sa otáča spolu s doskou, pôsobí na guličku, pokiaľ je v pohybe, sila Fc, ktorú nazývame Coriolisova sila. Táto guličku odchyľuje na stranu. Coriolisova sila vzniká keď sa teleso pohybuje v otáčajúcej sa sústave. Je kolmá na smer rýchlosti pohybujúceho sa telesa a na os otáčania rotujúcej sústavy. Pre každý pohyb v rovine kolmej na os otáčania má veľkosť určenú posledne uvedenou rovnicou.
Uvedený vzťah platí aj vtedy, keď rýchlosť v má v rovine kolmej na os otáčania iný smer než radiálny. Ak však zviera vektor rýchlosti v s osou otáčania iný ako pravý uhol, napr. α , potom sa podrobnejšími úvahami dá odvodiť pre Coriolisovu silu vzťah
Ak chceš, otestuj sa.
