Úvod

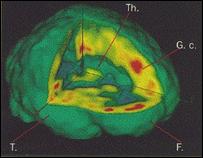
Magnetická rezonancia (MR) je jedným z mnohých fyzikálnych javov, objavených v posledných desaťročiach, ktorého význam v poslednom čase stúpol vďaka jeho rozšíreniu do viacerých oblastí života. Do povedomia širokej verejnosti sa dostal využitím jadrovej magnetickej rezonancie (NMR – z angl. nuclear magnetic resonance) v medicíne, kde sa používajú počítačové tomografy NMR pri kvalitnejšom diagnostikovaní rôznych chorôb.

Zopakujte si

• Vymenujte, kde ste sa s pojmom rezonancia stretli.
• Čo rozumiete pod pojmom rezonancia?
• Akým spôsobom dokážeme vyvolať rezonanciu?
• Čo podmieňuje magnetické vlastnosti niektorých látok?
• Ako sa správajú zmagnetizované telesá v magnetickom poli?

V súčasnosti poznáme viac druhov magnetickej rezonancie (MR), či už magnetických momentov elektrónov (elektrónová paramagnetická, elektrická, cyklotrónová, ferimagnetická, feromagnetická, antiferomagnetická, akustická paramagnetická, spin-vlnová rezonancia a iné), alebo magnetických momentov jadra atómu (jadrová magnetická rezonancia, kvadrupólová rezonancia, g -rezonancia, dvojná magnetická rezonancia a iné). MR sa využíva vo fyzikálnom, chemickom a biologickom výskume.

Vyhľadajte na Internete

• Pomocou niektorého z vyhľadávačov a zadaním kľúčových slov: nukleárna magnetická rezonancia získajte informácie o uvedenej problematike.

Domnievame sa, že vzhľadom na široké rozšírenie javu magnetickej rezonancie vznikla potreba vy svetliť zložité správanie sa častice vykazujúcej magnetický moment v stave magnetickej rezonancie nielen pre študentov vysokých škôl, ale i pre študentov stredných škôl. Pokúsme sa spoločne pochopiť fyzikálnu podstatu javu magnetickej rezonancie.

Jav magnetickej rezonancie

Vysvetliť a pochopiť zložité správanie sa častice s magnetickým momentom v stave rezonancie je možné na vedomostnej úrovni študentov vysokých škôl využitím vlastností rotujúcej sústavy, alebo riešením rovnice netlmeného harmonického pohybu. Na strednej škole sa však pokúsime o vysvetlenie na príklade elektrónovej paramagnetickej rezonancie. Vychádzajúc z planetárneho modelu atómu, elektrón obiehajúci okolo jadra vytvára vo svojom okolí magnetické pole, teda má orbitálny magnetický moment. Správanie sa častice vytvárajúcej svojim pohybom magnetický moment môžeme prirovnať ku správaniu sa telesa rotujúceho okolo svojej osi (gyroskopu), ktoré má moment hybnosti, v gravitačnom poli. Prirovnanie nám pomôže preklenúť bariéru v pochopení správania sa mikročastice, použijúc opis správania sa telesa, ktoré je študentom známe z vlastnej skúsenosti (napr. detská hračka vlk).

Pozorujte

• Roztočte detskú hračku „vĺčka“. Pozorujte jeho rotačný pohyb. Opíšte pozorovaný pohyb.

Samotný opis pohybu tuhého telesa okolo svojej osi vykonáme na základe analógie so zákonmi a fyzikálnymi veličinami opisujúcimi pohyb hmotného bodu po priamke. V Tab.1 sú po riadkoch napísané navzájom zodpovedajúce si fyzikálne veličiny a zákony charakterizujúce posuvný pohyb hmotného bodu a otáčavý pohyb tuhého telesa. Vo výklade pre študentov nie je potrebné používať vektorové veličiny a vektorový zápis rovníc. Všetky veličiny a vzťahy medzi nimi môžeme zapisovať v skalárnom tvare.

Rotujúce teleso (gyroskop) vykazuje moment hybnosti , ktorého smer a veľkosť sa zachováva ak na teleso nepôsobí gravitačné pole (zákon zachovania momentu hybnosti). Uvažujme teleso podoprené v osi otáčania mimo ťažiska. Gravitačné pole pôsobí v ťažisku telesa silou, ktorej moment má na teleso otáčavý účinok. Teleso vykonáva precesný pohyb, pri ktorom os otáčania opisuje kužeľovú plochu.

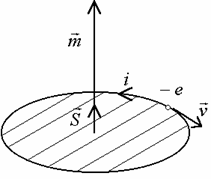
Magnetický moment možno definovať dvoma nezávislými spôsobmi, ktoré sa navzájom dopĺňajú: prvý spôsob definuje Ampérov moment ako súčin slučkového prúdu a plochy , ktorú prúd opisuje:

(vektor plochy je kolmý na plochu a má smer do polpriestoru, z ktorého obiehanie prúdu je opačný ako pohyb hodinových ručičiek) . Jednotka magnetického momentu je , Obr.1.

Druhý spôsob definuje Coulombov moment vychádza z existencie magnetického množstva (analógia k elektrickému náboju, ktorý vystupuje v definícii elektrického momentu v elektrostatike nasledovne: )

kde: je magnetické množstvo, -vektor so začiatkom v mieste záporného a koncom v mieste kladného náboja.

Vysvetlenie správania sa magnetického momentu v magnetickom poli vykonáme na základe analógie správania sa mechanických a magnetických veličín (magnetomechanický paralelizmu).

Teleso majúce súčasne mechanický a magnetický moment (ktoré sú kolineárne) sa pohybuje rovnako ako mechanický zotrvačník. Ak je upnuté tak, že je voľné (t. j. osi upevnenia prechádzajú ťažiskom telesa), tak gravitačná sila nemá účinok na pohyb telesa. Úlohu otáčavého účinku gravitačného poľa preberá magnetické pole s indukciou , pôsobiace na magnetický moment telesa momentom sily , ktorý bude mať tendenciu natočiť magnetický moment do smeru vektora .

Ak do definičného vzťahu pre moment sily dosadíme za vektor ramena sily vektor z definičného vzťahu pre magnetický moment , tak dostaneme nasledovný výraz pre moment sily pôsobiaci na magnetický moment:

,

alebo v skalárnom tvare

,

pretože indukcia je sila pôsobiaca na jednotkové kladné magnetické množstvo v magnetickom poli (analogicky, ako je definovaná intenzita elektrického poľa v elektrostatike) a je uhol, ktorý zviera vektor magnetického momentu a indukcie magnetického poľa . Magnetický a vlastný mechanický moment elementárnej častice je viazaný vzťahom:

kde g je gyromagnetický pomer. Rovnica (1.3) poukazuje na magnetomechanický paralelizmus, pod ktorým rozumieme fundamentálny súvis medzi magnetickým a mechanickým momentom častice.

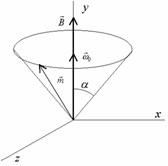
Ak na elektrón začne pôsobiť magnetické pole, vektor magnetického momentu začne precesovať okolo smeru vonkajšieho magnetického poľa podobne ako mechanický zotrvačník, Obr.2.

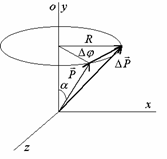
Pohyb takéhoto magnetického zotrvačníka môžeme teda prirovnať k otáčavému pohybu tuhého telesa okolo osi o , ktorý je spôsobený momentom vonkajších síl , pre ktorý platí analogický vzťah akým je zákon sily pre postupný pohyb (Tab.1):

.

Rovnicu (1.4) vieme upraviť, ak dosadíme za z definície uhlového zrýchlenia vzťah , pričom je krátky časový okamih:

.

Súčin predstavuje zmenu momentu hybnosti telesa pri otáčavom pohybe, tak ako je to znázornené na obr.3.

Vektor je moment hybnosti zotrvačníka súvisiaci s otáčaním sa zotrvačníka okolo svojej osi (moment hybnosti súvisiaci s precesiou je podstatne menší a v našich úvahách ho zanedbávame). Začiatok vektora je pevný a koncový bod vektora rotuje s uhlovou rýchlosťou a opíše dráhu po kružnici s polomerom za čas . Pre moment vonkajších síl platí vzťah, ktorý je z formálneho hľadiska analógiou Newtonovho pohybového zákona (Tab. 1):

. (1.6)

Pre moment vonkajších síl elektrónu nachádzajúceho sa v magnetickom poli s magnetickým momentom , platí rovnica (1.2). Pravé strany vzťahov (1.5) a (1.6) môžeme dať do rovnosti v skalárnom tvare:

. (1.7)

Zmenu hybnosti vyjadríme (obr.3) a pokračujeme v úprave rovnice pre výpočet uhlovej rýchlosti precesie magnetického momentu:

. (1.8)

Rovnicu (1.8) môžeme krátiť výrazom :

. (1.9)

Ak za dosadíme uhlovú rýchlosť , ktorú z rovnice vyjadríme, získame vzťah pre uhlovú rýchlosť precesie magnetického momentu:

, (1.10)

alebo

, (1.11)

Uhlová rýchlosť nezávisí od uhla precesie a volá sa Larmorova frekvencia , teda magnetický moment môže precesovať s ľubovolným uhlom precesie, ale závisí od veľkosti indukcie magnetického poľa , (obr.2).

Ak na magnetický moment precesujúci s uhlom precesie aplikujeme rotujúce magnetické pole kolmé na smer magnetické pole s frekvenciou tak, že bude v každom momente orientované zhodne s priemetom magnetického momentu do roviny kolmej na smer magnetického poľa (ide o kruhovo polarizovanú vlnu, ktorá je vo fáze s priemetom vektora do roviny xy), bude pole pôsobiť na magnetický moment momentom síl, ktorý bude zväčšovať uhol precesie. Bude dochádzať k absorbovaniu energie striedavého magnetického poľa, nastane rezonancia. Na absorbciu postačuje aj lineárne polarizovaná vlna (vektor magnetickej indukcie bude ležať na ľubovoľnej priamke kolmej na os precesie a okamžitá hodnota veľkosti magnetického poľa bude harmonickou funkciou času), ale podmienka nulového fázového posunu musí ostať zachovaná. Ak na magnetický moment aplikujeme striedavé magnetické pole kolmé na magnetické pole s frekvenciou rôznou v porovnaní s Larmorovou frekvenciou magnetický moment začne vykonávať nutáciu.

Demonštrácia javu magnetickej rezonancie

Na demonštráciu javu slúži zotrvačník (Obr. 4) upevnený v Cardanovom závese, tak aby všetky tri osi otáčania prechádzali ťažiskom zotrvačníka. Táto skutočnosť umožňuje splniť podmienku, aby gravitačná sila nepôsobila na zotrvačník otáčavým momentom. V osi zotrvačníka sa nachádza vhodný permanentný magnet.

Ak zotrvačník roztočíme okolo svojej osi malým elektromotorom, os rotácie bude zachovávať svoj smer, čo demonštruje zákon zachovania momentu hybnosti.

Zotrvačník vložíme do sústavy dvoch Helmholtzových cievok, ktoré vytvárajú navzájom kolmé magnetické polia, Obr. 4. Ak zapneme prúd do niektorej z cievok (neroztočený) zotrvačník sa otočí do smeru magnetického poľa, teda správa sa podobne ako magnetka kompasu reagujúca na smer magnetického poľa s tým rozdielom, že zotrvačník môže zaujať ľubovoľný smer, nie len smer vo vodorovnej rovine.

Ak zotrvačník roztočíme tak, aby os zotrvačníka zvierala nenulový uhol so zvislým smerom a zapneme zvislé magnetické pole, zotrvačník bude vykonávať precesný pohyb okolo smeru magnetického poľa. Frekvencia precesie bude závislá podľa vzťahu 1.10.

Ak do druhého páru Helmholtzových cievok privedieme striedavý prúd s frekvenciou odlišnou (výhodnejšia je použiť vyššiu) frekvenciou ako je frekvencia precesie, zotrvačník bude vykonávať nutáciu .

Vzhľadom na to, že frekvencia precesie je relatívne nízka, aby bola dobre pozorovateľná, podmienky pre rezonanciu je vhodné splniť nasledovne. Do cievok pre vytváranie magnetického poľa kolmého na os precesie privedieme namiesto prúdu harmonického priebehu vytvárajúceho priečne magnetické pole (ktorého fázu je obtiažne zosúladiť s fázou magnetického momentu) elektrický prúd obdĺžníkového priebehu, ktorý budeme ručne spínať podľa obr. 5., tak aby ním vytvorené striedavé magnetické pole bolo vo fáze s priemetom magnetického momentu do roviny kolmej na smer precesie.

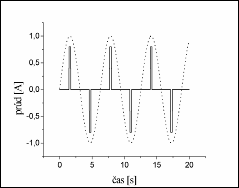
Uhol, ktorý zviera os zotrvačníka so smerom precesie sa zväčší, teda nastáva rezonancia. Ak priečne pole prestane pôsobiť, uhol precesie ostane konštantný (stacionárna MR).

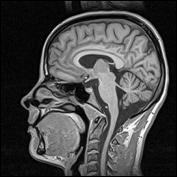
Uvedeným postupom možno demonštrovať základné vlastnosti magnetickej rezonancie. Pritom je potrebné mať na zreteli, že demonštrácia nevystihuje všetky detaily magnetickej rezonancie. Pri skutočných javoch magnetickej rezonancie ide o častice majúce vlastný mechanický moment hybnosti, je to ich základná vlastnosť. (Pri demonštrácii je zotrvačníku potrebné roztočením dodať mechanický moment, ktorý v čase vďaka treniu postupne klesá.) Okrem toho mikročastice nemôžu zvierať so smerom stacionárneho magnetického poľa ľubovoľný uhol, (tak ako makroskopiské teleso), priemet ich magnetického momentu do smeru magnetického poľa je kvantovaný. Mikroskopické magnetické momenty v látkových objektoch nie sú osamotené (tak ako magnetický moment zotrvačníka) a interagujú s okolitými magnetickými momentami tak, že im odovzdávajú absorbovanú energiu a po doznení vysokofrekvenčného poľa uhol precesie sa vráti na pôvodnú hodnotu vo veľmi krátkom čase. Túto skutočnosť je pomocou vyššie uvedeného prípravku možné demonštrovať tak, že prstenec na zotrvačníku mierne vysunieme z ťažiska, takže gravitačné pole bude prispievať k pohybu zotrvačníka otáčavým momentom pôsobiacim tak, že uhol precesie bude klesať. Po doznení impulzov priečneho magnetického poľa sa postupne uhol precesie zmenší až os zotrvačníka zaujme zvislý smer. Tento režim činnosti sa volá impulzná MR, pri ktorej sa meria relaxačný čas návratu magnetického momentu do pôvodného smeru. Na tomto princípe pracujú aj tomografy NMR používané v medicíne, keď v určitom bode mysleného rezu telom alebo skúmaným orgánom sa meria relaxačná konštanta jadrových spinov protónov vodíkových jadier atómov tvoriacich vodu tkanív. Postupne sa zmeria relaxačná konštanta bod po bode v riadku a neskôr sústava riadkov zaznamená celú rovinu rezu (podobne ako sa tvorí obraz na obrazovke televízneho prijímača). Hodnote relaxačnej konštanty sa priradí určitá farba pri farebnom zobrazovaní alebo určitý stupeň šedi pri čierno-bielom zobrazovaní. Takto sa zrekonštruuje obraz roviny rezu, z ktorého odborník rozozná poškodené tkanivo od zdravého.

Literatúra

[1] Rákoš, M.: Rádiospektroskopické metódy, Alfa, Bratislava, 1988

[2] Tirpák, A.: Elektromagnetizmus, Polygrafia SAV, Bratislava, 1999

[3] Chikazumi, S.: Physics of ferromagnetism, Oxford University Press, Oxford, 1997

[4] Füzerová, J., Kollár, P.: Demonštrácia javu magnetickej rezonancie, Zborník pedagogických príspevkov z vedeckej konferencie FYZIKA 2002, TU FEI-KF, Košice, s.14-16

[5] Füzerová, J., Kollár, P.: Vysvetlenie využitia javu magnetickej rezonancie v tomografickom NMR zobrazovaní pre študentov gymnázia, Zborník 13. konferencie slovenských fyzikov, 25.-28. 8. 2003, Smolenice, 119-120