Obsah

Dráha a čas voľného pádu

Pre jednoduchý prípad z pokoja voľne pusteného telesa, platí vzťah:

s = 1/2 g t²

s = dráha voľného pádu ; g = gravitačné zrýchlenie; t = čas voľného pádu

Dráha voľnéh opádu narastá s druhom mocninou času voľného pádu. Nasledujúca simulácia vysvetľuje, ako získame tento vzťah. Teleso naľavo sa pohybuje s konštantnou rýchlosťou, teleso napravo s konštantným zrýchlením.

Otázka:

Akú konštantnú rýchlosť potrebuje teleso naľavo, aby obe telesá dosiahli dno kocky v rovnakom časovom okamihu?

Rýchlosť telesa

Zmeňte rýchlosť telesa vľavo o
Δv = -10   -50; +10  +50 jednotiek.

Záver:

Rýchlosť zrýchľovaného telesa rastie z nuly na maximálnu hodnotu v_max kedy dosiahne dno kocky.

K prejdeniu tej istej dráhy s_max  počas rovnakého času sa teleso vľavo musí pohybovať konštantnou rýchlosťou v = v_max/2.

V tomto prípade je teleso veľmi rýchle na začiatku a príliš pomalé na konci. Je to vyvážené pretože rýchlosť zrýchleného teleso bude vzrastať lineárne z nulovej hodnoty na v_max.

Teleso vľavo, pohybujúce sa konštantnou rýchlosťou dosiahne počas časového intervalu t_max vzdialenosť:

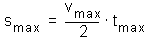
Tento vzťah je platný pre ľubovoľnú vzdialenosť a časový interval pokiaľ teleso štartuje z pokoja. Preto môžeme odstrániť indexi a dostaneme vzťah medzi vzdialenosťou pádu a časom pádu:

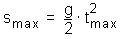
K zobrazeniu času, časovač, ako aj simulácia musia byť spustené.

Pre simuláciu platí: s_max = 2000 jednotiek; g = 10 jednotiek.

Nájdete zhodu medzi výsledkom simulácie a matematickým vzťahom stanoveným vyššie?

Stav beztiaže - Stav bez sily