ARCHIMEDOV   ZÁKON        späť

*  Teleso ponorené do kvapaliny je nadahčované vztlakovou silou, ktorej veľkosť sa rovná tiaži kvapaliny rovnakého objemu, ako objem ponorenej časti.

Možno overiť silomerom (A) alebo  pomocou rovnoramenných váh (B):
Varianta A:

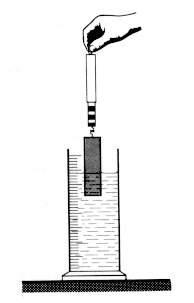
Pomôcky:
odmerný valec, silomer, závažie z hačikom, niť, voda.
Príprava a prevedenie:
    Odmerný vale naplníme vodou asi do dvoch tretín jeho výšky tak, aby  sa hladina kryla s niektorou ryskou.  Na silomer zavesíme na niť závažie a zistíme jeho tiaž G na vzduchu.  Potom závažie zavesené na silomeri ponoríme do vody vo valci a zistíme silu F. Z rozdielu hladín v odmernom valci pred a po ponorení závažia zistíme objem V závažia. Vypočítame tiaž vody G1  o objeme V (G1 = V.ro.g, ro je husstota vody)  a porovnáme  ju s rozdielom údajov  na silomeri: G - F.
                                  Zistíme:   G -F = G1
Záver: Závažie ponorené do vody je nadľahčované vztlakovou silou G -F, ktorá ma rovnakú veľkosť ako tiaž vody G1 rovnakého objemu ako je objem ponorenej časti V.

Varianta B:

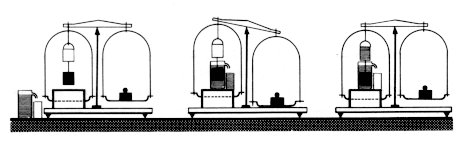Pomôcky: dutý a plný valec, rovnoramenné váhy, závažia , voda, kadička.
Postup a prevedenie: Presvedčíme sa, či možno plný valec zasunúť do dutého valca.  Pokiaľ nie musíme povrchy oboch valcov očistiť. Pokus prevedieme v nasledovných etapách:
1. Zasunutím plného valca do  dutého  ukážeme, že plný valec má rovnaký objem, ako je dutina dutého valca.
2. Dutý valec zavesíme na  háčik jedného ramena rovnoramenných váh a tie vyvážime. Získame tak tiaž telesa G. (pod telesom je  prázdna kadička).
3. Do kadičky pod telesom nalejeme vodu tak, aby bolo celé teleso ponorené. Rovnováva sa poruší.
4. Vyrovnanie váh dosiahneme tak, že budeme nalievať vodu do dutého valca. Rovnováha nastane, keď bude  valec naplnený vou až po okraj.
Záver: Teleso ponorené do kvapaliny je nadľahčované vztlakovou silou, ktorá má rovnakú veľkosť ako tiaž kvapaliny, ktorej objem sa rovná objemu kvapaliny telesom vytlačenej (objemu ponoreného telesa).

PLÁVANIE   A  POTÁPANIE SA - Dôsledok Archimedovho zákona

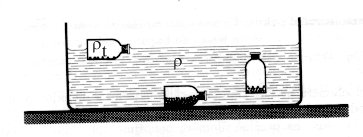
Na teleso ponorené v kvapaline pôsobí FG-ťiažová sila, a Fvz-vztlaková sila.
Ak označíme V objem ponoreného telesa, rot hustotu telesa, ro hustotu vody potom

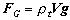
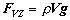
Môžu nastať tri prípady:
1. Pre 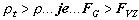    teleso klesá ku dnu
2. Pre 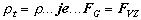    teleso sa voľne vznáša
3. Pre 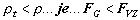    teleso súpa hore, až sa vynorí časťou nad voľnú hladinu. Rovnováha nastane, ak pre ponorenú časť s objemom V' platí:
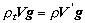  alebo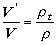 
Teleso sa ponorí do kvapaliny tým väčším objemom, čím je jeho hustota väčšia.